Inscription / Connexion Nouveau Sujet
Exo Dérivation complexe
Bonsoir à tous !
Albert est un fervent adepte de la plongée sous-marine. Alors qu'il se trouve en A et s'émerveille devant la beauté du paysage aquatique, il aperçoit au loin un requin d'une taille qui le dissuade de poursuivre plus avant son exploration des fonds marins et décide de rejoindre son bateau situé en B. À quel endroit doit-il rejoindre la surface pour que le temps de parcours soit minimal ?
Grâce à l'adrénaline secrétée par la portion médullaire de ses glandes surrénales, Albert se déplace à la vitesse de 7,2 km.h−1 sous l'eau et à la vitesse de 9 km.h−1 en surface. On supposera que la surface de l'eau est rectiligne, que la dérive due au courant est nulle et que la trajectoire d'Albert est une ligne brisée.
Pourriez-vous m'aider je ne vois pas comment commencer l'exercice !! Merci pour votre aide
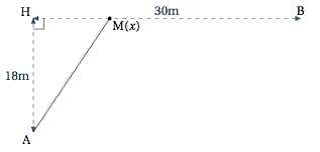
On doit te donner un dessin qui indique la profondeur à laquelle il est et la distance horizontale entre lui est son bateau ?
sinon c'est assez simple, tu appelles x la distance entre son bateau et le point où il émerge, tu calcules les durées plongée + nage de surface avec la formule T = D/V et tu minimises cette fonction de x.
Bonjour,
Je crois qu'il manque deux données à votre exercice:
- à quelle distance du bateau se trouve-t-il?
- quelle est sa profondeur au moment où il aperçoit le requin?
Je vais prendre deux exemples pour que vous compreniez:
Si jamais il est déjà en surface, il va nager uniquement en surface.
Si il est situé pile en dessous du bateau, il va nager uniquement vers le haut.
Donc il manque vraiment ces deux paramètres.
Bonsoir !
Sans un dessin montrant où sont impossible de t'aider ! Il faudrait avoir la distance horizontale entre
et la profondeur de
.
En notant le point d'émergence à une distance
de
tu calcules la distance
et tu essaies de trouver la valeur de
qui rend minimal le temps
.
J'ai supposé que le trajet sera situé dans le plan vertical contenant ce qui demande à Albert des talents de géomètre (et un sang froid exemplaire) pour rester dans ce plan. Bref je pense qu'il manque beaucoup de données.