Inscription / Connexion Nouveau Sujet
Exo Maths (1erS) (statestiques)
Bonjour,
En effet je suis en train de faire un devoir de maths sur les statestiques
voici l'enonce:
1. Completer le tableau de la serie avec les classes, les effectifs, les frequences et les fréquences cumu- lees croissantes.
2. Quelle est la classe qui contient la mediane ? celle qui contient le premier quartile ? celle qui contient le troisième quartile ? celle qui contient le premier decile ? celle qui contient le neuvieme decile ?
3. Déterminer la moyenne x et l'écart-type s. Quelles sont les classes incluses dans l'intervalle [x − 2s ; x + 2s ] ? La reunion de ces classes represente quel pourcentage de la population ?
4. Construire la courbe des fréquences cumulees croissantes.
5. En deduire une estimation graphique de la médiane, le premier quartile et le troisieme quartile de la
serie statistique
Ce que j ai mis comme reponses
☟
Question 2:
J'ai fait un tableau comme ca
| Quartile | x | Effectifs | Effectifs cummule croissants | frequance | frequance cumulee croisante |
| [0;10[ | 10 | 10 | 10/500 = 0,02 | 10/500 = 0,02 | |
| [10;20[ | 10 | 20 | 10/500= 0,02 | 20/500= 0,04 | |
| [20;30[ | 20 | 40 | 20/500= 0,04 | 40/500= 0,08 | |
| [30;40[ | 20 | 60 | 20/500= 0,04 | 60/500= 0,12 | |
| [40;50[ | 40 | 100 | 40/500= 0,08 | 100/500= 0,2=1/5 | |
| Q1 | [50;60[ | 60 | 160 | 60/500= 0,12 | 160/500= 0,32 |
| [60;70[ | 60 | 160 | 80/500= 0,16 | 240/500= 0,48 | |
| Mediane | [70;80[ | 90 | 330 | 90/500= 0,18 | 330/500= 0,66 |
| [80;90[ | 70 | 400 | 70/500= 0,14 | 400/500= 0,8 | |
| [[90;100 | 30 | 430 | 30/500=0,06 | 430/500=0,86 | |
| [100;110[ | 20 | 450 | 20/500=0,04 | 450/500=0,9 | |
| [110;120[ | 20 | 470 | 20/500=0,04 | 470/500= 0,94 | |
| [120;130[ | 10 | 480 | 10/500= 0,02 | 480/500= 0,96 | |
| [130;140[ | 10 | 490 | 10/500=0,02 | 490/500=0,98 | |
| [140;150[ | 5 | 495 | 5/500=0,01 | 495/500=0,99 | |
| [150;160[ | 5 | 500 | 5/500=0,01 | 500/500=1 |
ensuite
500=2k car paire ??
Mediane (X250 + X251) /2 => {70;80}
Q1= X125 = [50;60]
Q3= X375= [80;90]
1 er decile = x500/10=X50=[30;40]
9eme decile =x 500*3/10 = X450 = [100;110]
| x | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 | 135 | 145 | 155 |
| effectifs | 10 | 10 | 20 | 20 | 40 | 60 | 80 | 90 | 70 | 30 | 20 | 20 | 10 | 10 | 5 | 5 |
Maintenant je peux calculer la moyenne
x= ((10*5)+(15*10)+(25*20)+(35*20)+(45*40)+(55*60)+(65*80)+(75*90)+(85*70)+(95*30) +(105*20)+(115*20)+(125*10)+(135*10)+(145*5)+(155*5) ) /500
x=71,5
Pour calculer l'ecart type je calcule la variance d'abord
V=((10*5)2+(15*10)2+(25*20)2+(35*20)2+(45*40)2+(55*60)2+(65*80)2+(75*90)2+(85*70)2+(95*30)2 +(105*20)2+(115*20)[/sup]+(125*10)[sup]2+(135*10)2+(145*5)[/sup]+(155*5)[sup]2 ) /500= 290467,5
et ensuite 𝜎=√290467,5=538,950369
Par contre c'est quoi les classes ??? dans la Question 3 🤔
Et la courbe bas je peut pas la costruir ici
donc Q4 et 5 je laisse sans reponse mais s'il y a quelle quun qui peut m'aider ca serais super
Merci d;avance de votre aide
bonjour
pour être sure de bien comprendre : c'est à partir de l'histogramme que tu as rempli le tableau ?
quelles colonnes étaient déjà remplies dans ce tableau (la colonne x?) ?
ou bien c'est toi qui a fait le découpage en classes ?
les classes, ce sont les intervalles de x (colonne des x)
je n'ai pas vérifié tes calculs, il faut auparavant être sûr des effectifs,
et là, ils ne me semblent pas corrects
par ex :
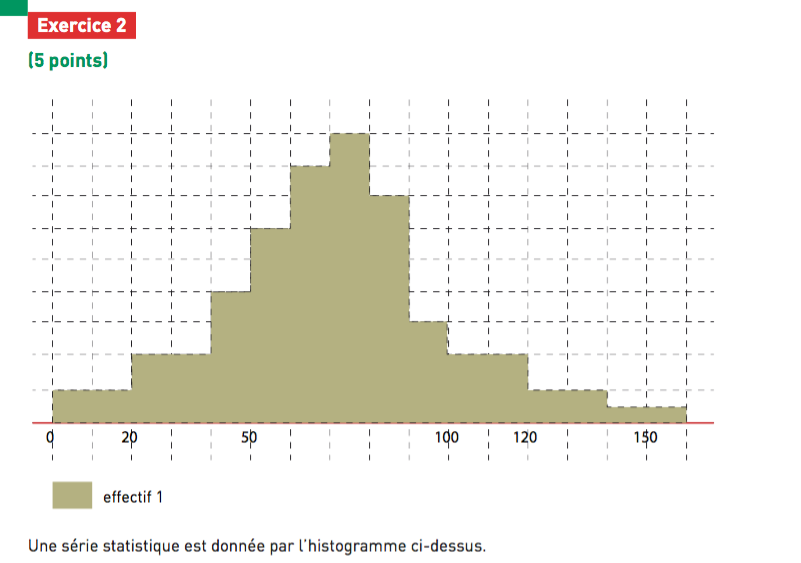
classe [0;10[, l'effectif est 1 et non pas 10 : la légende de l'histogramme dit : une "case" de la grille = 1
pour la 4) jette un oeil ici ![]() exercices de statistiques, tu as des exemples corrigés
exercices de statistiques, tu as des exemples corrigés
==> pour ton exo, il faudra prendre les fréquences cumulées croissantes, (et non pas les effectifs c.c.)
tes calculs : les démarches sont les bonnes
moyenne, Q1, médiane, Q3 : les résultats sont justes, mais pas les calculs.
==> calculs à reprendre, donc, avec le bon découpage des classes et les effectifs rectifiés.
bonjour
pour être sure de bien comprendre : c'est à partir de l'histogramme que tu as rempli le tableau ?
quelles colonnes étaient déjà remplies dans ce tableau (la colonne x?) ?
ou bien c'est toi qui a fait le découpage en classes ?
[/i]
bas la j ai rempli moi meme oui
bonjour
je n'ai pas vérifié tes calculs, il faut auparavant être sûr des effectifs,
et là, ils ne me semblent pas corrects
par ex :
classe [0;10[, l'effectif est 1 et non pas 10 : la légende de l'histogramme dit : une "case" de la grille = 1
bas ici le truc est que si je prends 1 bas les deux dernier intervalles je devrais prendre 0,5 ?? Mais ca ne semble pas super c estait pour ca que j ai pris 10 et non 1 🤔
tes calculs : les démarches sont les bonnes
moyenne, Q1, médiane, Q3 : les résultats sont justes, mais pas les calculs.
==> calculs à reprendre, donc, avec le bon découpage des classes et les effectifs rectifiés.
j ai pas trop cmpris la ... car en effet je n'ai pas fait vraiment les calcules pour les quartiles j'avais juste pris les valeur de x 125et 375 c'est faux?
Mais le reste : decile , mediane, et la question 3 ???
Merci d'avance
le découpage en classes :
si l'énoncé ne t'impose pas déjà les classes, ne te donne aucune consigne,
tu peux effet faire un découpage de 10 en 10.
en revanche, pour les effectifs, ce que tu as fait est faux.
la légende dit : 1 case = effectif de 1
ce serait toutefois intéressant de savoir ce que représente cette série statistique.
on lit : entre 140 et 150, l'effectif est de 0.5, et pareil 150 et 160.
==> s'il s'agit de personnes, on peut trouver plus logique de regrouper les 2 classes en 1 classe unique [140;160[ effectif 1
revois donc les effectifs de chaque classe en comptant les "cases" pour chaque intervalle.
sauf erreur, l'effectif total est N=50 --- et non pas 500
... et ça change tout 
"pour les quartiles j'avais juste pris les valeur de x 125et 375 c'est faux? "
ce serait juste si l'effectif était de 500 (1/4 de 500, puis 3/4 de 500),
mais l'effectif total n'est pas de 500.
montre les effectifs que tu trouves avant de te lancer dans les calculs
je vérifierai si tu veux.
n'aies pas trop de regret, il y avait une erreur sur cette ligne :
[60;70[ 60 160 80/500= 0,16 240/500= 0,48 --- ce n'était pas 60 et 160 , mais plutôt 80 et 240
les corrections seront assez simples à faire, puisque tu avais - à tort - multiplié les effectifs par 10 : il te suffit de tous les diviser par 10...
| x | effectifs | effectifs c.c. | frequance | frequance c.c. | |
| [0;10[ | 1 | 1 | 1/50 | 1/50 | |
| [10;20[ | 1 | 2 | 1/50 | 2/50 | |
| [20;30[ | 2 | 4 | 2/50 | 4/50 | |
| [30;40[ | 2 | 6 | 2/50 | 6/50 | |
| [40;50[ | 4 | 10 | 4/50 | 10/50 | |
| Q1 | [50;60[ | 6 | 16 | 6/50 | 16/50 |
| [60;70[ | 8 | 24 | 8/50 | 24/50 | |
| [70;80[ | 9 | 33 | 9/50 | 33/50 | |
| [80;90[ | 7 | 40 | 7/50 | 40/50 | |
| [90;100[ | 3 | 43 | 3/50 | 43/50 | |
| [100;110[ | 2 | 45 | 2/50 | 45/50 | |
| [110;120[ | 2 | 47 | 2/50 | 47/50 | |
| [120;130[ | 1 | 48 | 1/50 | 58/50 | |
| [130;140[ | 1 | 49 | 1/50 | 49/50 | |
| [140;150[ | 0,5 | 49,5 | 0,5/50 | 49,5/50 | |
| [150;160[ | 0,5 | 50 | 0,5/50 | 50/50 |
voila j ai tout divise pas 10
regarde si c est bien
il y avait une erreur sur cette ligne :
[60;70[ 60 160 80/500= 0,16 240/500= 0,48 --- ce n'était pas 60 et 160 , mais plutôt 80 et 240
.
la j ai pas trop compris ce que tu veux dire
ca viens d ou cette ligne au faite???
fréquence avec un "e" 
erreur de frappe sans doute sur cette ligne : [120;130[ 1 48 1/50 58/50 ------- 48 et non 58
hormis ça, c'est juste.
tu peux reprendre les calculs du reste.
et pour les fréquences, tu peux aussi les mettre sous forme décimale, comme tu avais fait sur ton 1er tableau (en fait, elles ne changent pas : 0.02 0.02 0.04 etc.)
ps : c'est la ligne de ton tableau dont j'ai fait un copié-collé. (on ne voit pas les séparations du tableau)
| x | effectifs | effectifs c.c. | frequance | frequance c.c. | |
| [0;10[ | 1 | 1 | 1/50 | 1/50 | |
| [10;20[ | 1 | 2 | 1/50 | 2/50 | |
| [20;30[ | 2 | 4 | 2/50 | 4/50 | |
| [30;40[ | 2 | 6 | 2/50 | 6/50 | |
| [40;50[ | 4 | 10 | 4/50 | 10/50 | |
| Q1 | [50;60[ | 6 | 16 | 6/50 | 16/50 |
| [60;70[ | 8 | 24 | 8/50 | 24/50 | |
| mediane | [70;80[ | 9 | 33 | 9/50 | 33/50 |
| Q3 | [80;90[ | 7 | 40 | 7/50 | 40/50 |
| [90;100[ | 3 | 43 | 3/50 | 43/50 | |
| [100;110[ | 2 | 45 | 2/50 | 45/50 | |
| [110;120[ | 2 | 47 | 2/50 | 47/50 | |
| [120;130[ | 1 | 48 | 1/50 | 58/50 | |
| [130;140[ | 1 | 49 | 1/50 | 49/50 | |
| [140;150[ | 0,5 | 49,5 | 0,5/50 | 49,5/50 | |
| [150;160[ | 0,5 | 50 | 0,5/50 | 50/50 |
ce que j ai mis en verts c est ce que je viens de recalculer
et j ai faite une redaction comme ceci :
La classe qui cntien la mediane est:
deja Nest pair donc N=2k
50=2k donc pour avoir 50 k doit etre = a 25
donc 50=2*25
or d'apres le cour lla mediane est la demie somme de terme de rang k et k+1
donc c est 25 et 25+1+26
donc c est linterval [70;80]
(je suis pas sur que c est jsute la redaction comme ca )
Pour calculer Q1 on fait
50*1/4=12,5
or 12,5 n est pas entier donc on l'arondie just'qua 13 vue que d'apres les cour Q1 est tel qu'au moins 25% de donee soyent
 a nombre Q1
a nombre Q1
Donc c est l'interval [50;60] d'apres le tableau
Q3 = 50*3/4=37,5 on fait de mem et ca nous donner [80;90]
voila mais pour le decile je m'embrouille :\
ok pour le tableau
pour les paramètres de position : ici la variable est continue (classes).
pour déterminer la classe qui contient la médiane, c'est plus simple que ce que tu as fait :
(d'après les définitions du cours)
- la médiane partage l'effectif en 2 parts égales
N =50 donc N/2 = 25
dans le tableau, on cherche où se trouve la 25ème valeur dans les effectifs cumulés croissants :
on lit classe [70;80[
et c'est fini pour répondre à la question posée.
- q1 --> N/4 = 12.5 --> on cherche la 13ème valeur --> q1 est dans la classe [50;60[
- q3 --> 3N/4 = 37.5 --> on cherche la 38ème valeur --> q1 est dans la classe [80;90[
- d1 --> N/10 =5 --> on cherche la 5ème valeur --> d1 est dans la classe ....?
- d9 --> 9N/10 =.... --> on cherche la .....ème valeur --> d9 est dans la classe ....?
- d1 --> N/10 =5 --> on cherche la 5ème valeur --> d1 est dans la classe [30;40[?
- d9 --> 9N/10 =.... --> on cherche la 45ème valeur --> d9 est dans la classe [100;110[?
c 'est juste?
mais comment je fais pour la question 3???
je prendsles intervales par exemple [0;10[ et je prends 5 comme valeur comme j ai ecris dans le tableau de uxieme que j ai faite danquand j ai cree le topic ??
et j' aditionne tout sa puis divise par 50 et ensuite je calcule la variance et l ecart type ??
ok pour d1 et d9
moyenne : oui, fais comme tu avais fait au début, en prenant les centres de classe.
variance : applique la formule que tu as dans le cours (tu me la rappelles?)
tu l'avais mal appliquée au début.
bas Variance(x) = (x1-x(avec le trait au dessus ) )2 +(x2-x(avec le trait au dessus ) )2 ........(xp-x(avec le trait au dessus ) )2 / n1+n2.....np
donc je prends le tableau et je change les effectifs?
| x | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 | 135 | 145 | 155 |
| effectifs | 1 | 1 | 2 | 2 | 4 | 6 | 8 | 9 | 7 | 3 | 2 | 2 | 1 | 1 | 0,5 | 0,5 |
la moyenne sera
Me=(5*1)+(15*1)+(25*2)+(35*2)+(45*4)+(55*6)+(65*8)+(75*9)+(85*7)+(95*3)+(105*2)+(115*2)+(125*1)+(135*1)+(145*0,5)+(155*0,5)/50=3499,05
ecart type= 𝜎=√3499,05=52,1527683
Est que c est correct??
[x − 2s ; x + 2s ] = [3499,05-2*52,1527683; 3499,05+2*52,1527683]=[3394,74446;3603,35554]
c'est pour la suite de la question
mais je suis pas trop sur que ca soit juste
car ca me semble les valeurs sont un peu grandes
c'est somme si je me suis trompee dans le calcul de la moyen et de l'equart type 🤔
car au faite on doit dire quelles sont les classes includes dans cette interval que je viens de "trouver"
j'au encore un exo deposee sur ce forum quand on aura fini avec celui ci tu pourrais aller voir l'autre car au faite il y a eu quellequ'un qui a ecrit un commentaire mais apres rien , merci d'avance
![]() Exercice de Maths 1erS (STATISTIQUES)
Exercice de Maths 1erS (STATISTIQUES)
2 formules équivalentes à disposition pour la variance :
ou bien
... tu n'as appliqué ni l'une ni l'autre; donc résultat faux.
d'autant plus que l'écart-type est la racine carrée de la variance, pas de la moyenne.
pour la moyenne, revois aussi ton calcul.
penses-tu raisonnablement que pour une variable qui s'étale de 0 à 160, on puisse avoir une moyenne de presque 3500 ?
je dois m'absenter.
a+
ah oui c'est vrai j 'ai du n'importe quoi
mais avec la moyenne je vois pas trop l'erreur car j ai fait quoi j ai multipliee chaque valeur par son effectifs et j'ai tout divisee par 50 (effectif total)
et ce calcul jai mis a excel et il m'a donee ca
mais oui effectivement je suis d'accord que ca parriat bizzare
j'ai refait ca donne ca si je me trompe pas :
(5*1)+(15*1)+(25*2)+(35*2)+(45*4)+(55*6)+(65*8)+(75*9)+(85*7)+(95*3)+(105*2)+(115*2)+(125*1)+(135*1)+(145*0,5)+(155*0,5)=3575
3575/50=71,5
donc effectivement c'etati faux
donc la moyenne est 71,5
du coup pour la variance j'ai fait ca
V(x)=(1*(5-71,5)^2+1*(15-71,5)^2+2*(25-71,5)^2+2*(35-71,5)^2+4*(45-71,5)^2+6*(55-71,5)^2+8*(65-71,5)^2+9*(75-71,5)^2+7*(85-71,5)^2+3*(95-71,5)^2+2*(105-71,5)^2+2*(115-71,5)^2+1*(125-71,5)^2+1*(135-71,5)^2+0,5*(145-71,5)^2+0,5*(155-71,5)^2)/50=830,75
Est que la c'est juste ??
[13,9; 129,2] oui
regarde quelles classes sont concernées par ces valeurs de x,
ainsi que leurs effectifs correspondants.
la somme de ces effectifs-là represente quel pourcentage de la population totale ?
ok, je repasse te lire + tard.
a quoi correspnd cette interval ?? A x?
==> 01-03-17 à 12:12 : regarde quelles classes sont concernées par ces valeurs de x 
l'intervalle [13,9; 129,2] représente toutes les valeurs de x comprises entre 13.9 et 129.2 (au sens large)
donc toutes les classes de ...? à ...?
La reunion de ces classes represente quel pourcentage de la population ?
je crois que oui
fin je suis pas sur
aah oui c'est vrai
alors je crois que c'est 47*100/50=94%
Juste?
Et je voudrais aussi metter l'image du graphique mais a chaque fois ca depasse les 80ko :/

 830,75 = 28,8227341
830,75 = 28,8227341
