Inscription / Connexion Nouveau Sujet
Exploiter une représentation graphique.
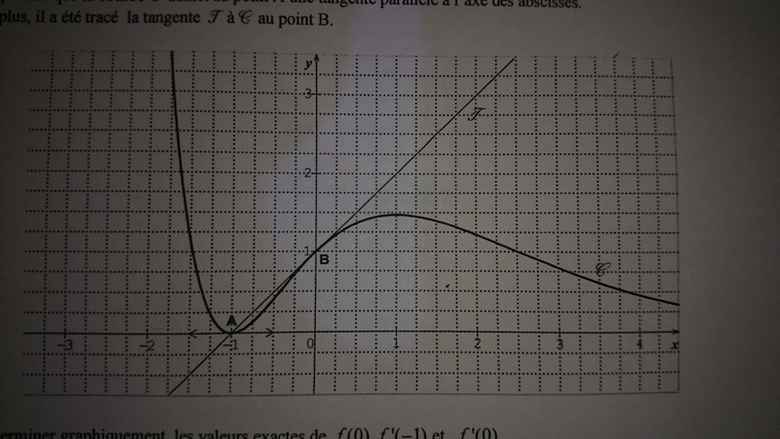
Dans un repère orthonormé, on a tracé la courbe C représentative d'une fonction f définie et dérivable sur IR.
On précise que la courbe C admet au point A une tangente parallèle à l'axe des abscisses.
De plus, il a été tracé la tangente T à C au point B.
1)a) Déterminer graphiquement les valeurs exactes de f(0), f'(-1) et f'(0).
b) Déterminer une équation de la tangente T à C au point B.
2)On admet que la fonction f est définie sur IR par f(x)=(ax2+bx+c)e-x , où a,b et c sont trois nombres.
Déterminer les nombres a,b,c à l'aide des résultats de la question 1.
3) Etudier les variations de f ; puis dresser son tableau de variation.
4) Dans cette question on se propose d'étudier la position relative de la courbe C et de la tangente T à C en B.
a) justifier que le problème revient a déterminer le signe de (x+1)φ(x), ou φ est la fonction définie sur IR par: φ(x)=(x+1)e-x-1 .
b) calculer φ'(x), puis φ"(x). En déduire les variations de φ' sur IR.
c) En utilisant la question précedente, déterminer le signe de φ'(x), puis les variations de φ sur IR. (les limites de φ ne sont pas demandées).
d) En déduire le signe de φ(x), puis conclure quant à la position de C et T.
5) On admet que la fonction f définie sur IR par f(x)=(x+1)2e-x .
Déterminer les nombres réels a,b,c tels que la fonction F définie sur IR par : F(x)=(ax2+bx+c)e-x soit une primitive de f sur IR.
J'ai vraiment besoin d'aide pour ce DM qui est a rendre a la rentrée
BONJOUR ?
MERCI D'AVANCE ou S'IL VOUS PLAIT ?
Lire ceci : ------> ![]() Sujet ancien- ne plus donner ce lien-merci les gestionnaires de ce forum n'ont pas écrit ce topic, juste pour faire joli dans le décors !
Sujet ancien- ne plus donner ce lien-merci les gestionnaires de ce forum n'ont pas écrit ce topic, juste pour faire joli dans le décors !
et cela : ------> ![]() [lien]
[lien]
Bonnes lectures ! ☺
Tu y liras qu'il faut :
Ne PAS DONNER SON ENONCE BRUT, écrire également les pistes de réflexion, les problèmes rencontrés,
Ne n'arrive pas la 1ère question je ne peux donc pas faire la suite. Je ne comprends pas comment on peut déterminer graphiquement une dérivé
f(0), c'est l'ordonnée du point B dont l'abscisse est égale à 0. On voit sur le graphique que cette ordonnée est égale à 1. Donc f(0) = 1.
f '(- 1), c'est la pente de la tangente à la courbe au point d'abscisse - 1 . On voit que cette tangente est horizontale. Donc f '(- 1) = 0.
Etc.
Cours de seconde :
un point M de coordonnées (x ; y) est un point de la représentation graphique de la fonction f si et seulement si y = ....
Bonjour,
j'ai moi aussi cet exercice à rendre.
J'ai réussi la question 1 a et b, mais pour la 2ème question je ne suis pas vraiment sure de mes résultats étant donné que si je fais tracer la courbe que la fonction f que j'ai trouvé grâce à mes valeurs pour a, b et c, la courbe donnée par ma calculette ne ressemble pas au graphique donné.
Mes valeurs sont : a = -1
b = 2 et c = 1
Est ce que vous pourriez me dire si ça vous paraît juste et si non, comment trouver les bonnes valeurs ?