Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Exponentielle de base a

Posté par
hello18 03-05-11 à 23:05

Bonsoir,
Je bloque sur un exercice...
1) Démontrer que la fonction f(x)=xa (ou xa=ea.lnx) est dérivable sur R+* et que sa dérivée est a.xa-1.

J'ai dit que la fonction f(x) est de la forme eu (avec u(x)=a.lnx) Donc f'(x)=a/x . ea.lnx
Mais ce n'est pas ça car on donne la dérivée un peu plus loin ...
Merci d'avance de votre aide.

Posté par
bibere : Exponentielle de base a 03-05-11 à 23:12

Bonsoir,

Quand tu as f'(x)=a/x .exp(a.ln(x))  tu peux écrire exp(a.ln(x))=xa

Donc f'(x)=(a/x)*xa  et on sait également que 1/x=x-1

f'(x)=a.xa.x-1

f'(x)=a.xa-1

Posté par
hello18re : Exponentielle de base a 03-05-11 à 23:22

merci beaucoup!!
Et pour dire qu'elle est dérivable sur R+*, on peut dire que
a/x est dérivable sur R* ; que la fonction expo est dérivable sur R Et que a.lnx est dérivable sur R+* DONC par composition, f'(x) est dérivable sur R+*.

Posté par
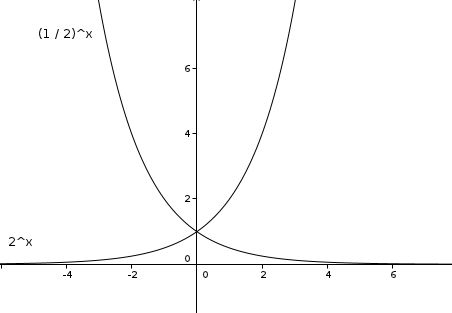
hello18re : Exponentielle de base a 03-05-11 à 23:52

J'ai une autre petite question, peut on dire que les fonctions f(x)=2x et g(x)=(1/2)x sont symétriques ?

Posté par
dhaltere : Exponentielle de base a 03-05-11 à 23:56

f(-x)= 2^{-x}=\frac{1}{2^x}=\frac{1^x}{2^x}=(\frac12)^x=g(x)
oui, on peut le dire

Exponentielle de base a

Posté par
hello18re : Exponentielle de base a 04-05-11 à 00:13

Merci !
Par contre, j'ai une nouvelle question
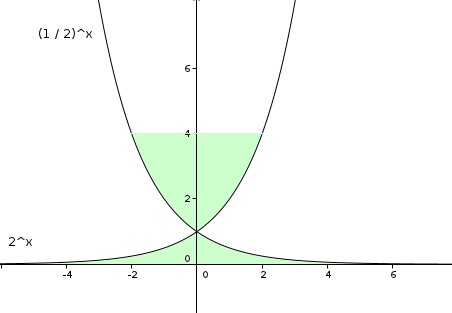
je dois calculer l'aire verte. Je pense avoir une idée : Calculer seulement une partie (par ex celle entre 0 +00) et la multiplier par deux.
Pour le petit morceau en bas, je pense que j'arriverais à le faire mais comment faire pour la partie du haut ?
mErci d'avance

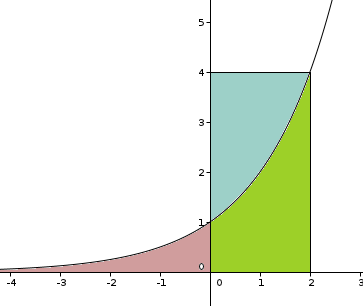
Exponentielle de base a

Posté par
dhaltere : Exponentielle de base a 04-05-11 à 00:19

Exponentielle de base a

l'intégrale facile à calculer est la verte
tu veux la bleue
mais vert + bleu est un rectangle lui aussi facile à calculer
tu feras la différence des deux.

Posté par
hello18re : Exponentielle de base a 04-05-11 à 00:31

Ah ! astucieux !Merci beaucoup. Je pense que je devrais m'en sortir tout seul maintenant.
Une dernière chose, peux-tu regarder ma rédaction :

Citation :

f(x)=xa (ou xa=ea.lnx)
Et pour dire qu'elle est dérivable sur R+*, on peut dire que
a/x est dérivable sur R* ; que la fonction expo est dérivable sur R Et que a.lnx est dérivable sur R+* DONC par composition, f'(x) est dérivable sur R+*.

Posté par
dhaltere : Exponentielle de base a 04-05-11 à 08:08

Pour tout couple (b;a)\in\mathbb{R}^{*+}\,\times\,\mathbb{R}, on définit b^a=e^{(a\ln(b))}

il est important de voir que cette expression n'est effectivement définie dans le cadre des nombres réels que pour b>0

(on peut aussi définir ces expressions dans le cas des nombres complexes, mais c'est une toute autre histoire)

cette définition est homogène avec les propriétés des exponentielles, en particulier celles-ci :
e^{(a\ln(b))}=(e^{\ln(b)})^a=(b)^a

pour tout a\in\mathbb{R}, on définit la fonction f_a par
f_a\,:\qquad\begin{array}{ccl} \\ \mathbb{R}^{+*}&\longrightarrow&\mathbb{R} \\ x&\longrightarrow&f_a(x)=x^a=e^{(a\ln(x))}\end{array}

Alors cette fonction sous la seconde forme est la composition de deux fonctions :
f_a=h\circ g
définies ainsi
g\,:\qquad\begin{array}{ccl} \\ \mathbb{R}^{+*}&\longrightarrow&\mathbb{R} \\ x&\longrightarrow&g(x)=a\ln(x)\end{array}
et
h\,:\qquad\begin{array}{ccl} \\ \mathbb{R}&\longrightarrow&\mathbb{R} \\ x&\longrightarrow&h(x)=e^{x}\end{array}

La fonction g est définie, continue et dérivable sur son domaine de définition et est à valeurs dans l'ensemble des réels qui est le domaine de définition de h

La fonction h est définie, continue et dérivable sur son domaine de définition

La fonction composée f_a=h\circ g est alors définie, continue et dérivable sur le domaine de définition de g

la fonction dérivée de f_a, notée f_a', s'obtient par la formule de la dérivée :
f_a'(x)=(h\circ g)'(x)=g'(x) \times[h'\circ g](x)
avec
g(x)=a\ln(x)\rightarrow g'(x)=\frac ax=ax^{(-1)} \\ h(x)=e^x\rightarrow h'(x)=e^x

donc
f_a'(x)=ax^{(-1)}\times e^{a\ln(x)}
l'expression x^{(-1)} est une expression particulière de la famille de fonctions f_a : f_{-1}(x)=x^{(-1)}=e^{(-\ln(x))}

donc la fonction dérivée f_a' s'exprime ainsi :
f_a'(x)=ae^{(-\ln(x))}\times e^{a\ln(x)}
et les propriétés des exponentielles nous permettent d'écrire que
f_a'(x)=ae^{(-\ln(x)+a\ln(x))} \\ f_a'(x)=ae^{((a-1)\ln(x))}

L'expression e^{((a-1)\ln(x))} est une expression particulière de la famille de fonctions f_a : f_{a-1}(x)=x^{(a-1)}=e^{((a-1)\ln(x))}

donc la fonction dérivée f_a' s'exprime ainsi :
f_a'(x)=ax^{(a-1)}

et voilà la démonstration complète de cette formule, un vrai roman, n'est-ce pas, mais au moins il ne reste aucune ambiguïté

je t'avoue que ton prof n'en attend sûrement pas tant, à toi de prendre ce qui te parait judicieux.

Posté par
hello18re : Exponentielle de base a 04-05-11 à 15:18

Je n'attendais pas une réponse aussi complète ! Mais merci beaucoup tout de même !


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !