Bonjour,

C'est cela ta fonction :   ?

Bonjour,

Je suppose que ta fonction est f(x) = (9/2)e^-2x - 3e^-3x vu la dérivée que tu as fais

Je suis d'accord sur la première partie: ((9/2)e^-2x)' = -9e^-2x
En revanche, quand tu vas dériver 3e^-3x, selon la formule (eu)'= u'e^u, tu vas avoir 3(3e^-3x) = 9^e-3x
Donc avec ta factorisation: 3(-3e^-2x+3e^-3x)

  ?

(sans le ?)

merci  ,  mais  est  ce  +  ou  -  ?

+ ou - quoi ?

Théoriquement, tu sais que (x ; e^x > 0). Par conséquent, tu sais que le signe de ta dérivée dépendra uniquement de (e^x-1-1) étant donné que 9e-2x > 0. Il te reste donc à déterminer le signe de (e^x-1-1)

Oops, légère erreur de ma part: le signe ne dépendra que de (e^-x-1) étant donné que 9e^-2x >0

merci   excusez  le  +  ou -  je   n'ai  pas  vu  de  suite  que  vos  reponses

etaient  semblables !

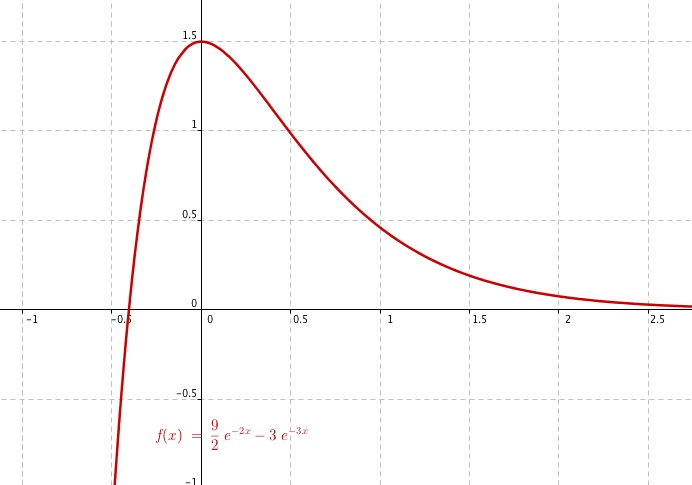
bonsoir,on  demande de  calculer  les points  d'intersection  de  la  courbe C   avec  les  axes  du  repere

j'ai  trouve  sur  les  ordonnées (0, 3/2)

sur  les  abcisses  mon  resultat  est  incoherent  quand  je  le  visionne  sur  "geogebra

(j'ai  mis  la  fonction  = 0 )   merci

Bonjour,

Non, ce n'est absolument pas cela le résultat.

On a

Qu'as-tu fait pour trouver ton résultat ?

bonjour,  merci.  est ce que mon point sur l axe des ordonnées. est. faux (+3/2). est. faux?

Sur la courbe tracée sur. geogebra il paraît.  juste?  la courbe coupe l axe. des. abscisses

entre 0 et. _1. ! est ce que je peux. la. joindre ?     merci

Je ne comprends pas ta question.

bonjour  merci  je  me  suis  peut  etre  mal  exprimé

les  points  d'intersection  de  la  courbe  avec  l'axe  

des  ordonnées  est  +  3/2

avec  l'axe  des  abcisses    ln2/3  avec  le  caicul  suivant

9/2 exp (-2x) = 3exp(-3x)

3/2exp(-2x)=exp(-3x)

3/2exp(0)=exp(-x)
3/2=exp(-x)

exp(x)=2/3     x=ln2/3  =-0,405    Merci  de  votre aide

Tout est bon,  sauf que c'est plutôt comme cela :

9/2 exp (-2x) = 3exp(-3x)

3/2exp(-2x)=exp(-3x)

3/2=exp(-x)

-x=ln3/2  

x=-ln3/2=-(ln3-ln2)=-ln3+ln2=ln(2/3)

bonjour,  Est ce que. mon calcul est. bon. quand. même ?

puis je encore abuser de votre aide. ?

pour   f(x)=x(1_lnx).  f' =_ lnx ?

je ne sais pas. calculer. la. primitive. de. f(x).    merci

Non ton calcul n'est pas bon, voir mon dernier post.

C'est quoi tes _ ?

Merci
Les _ sont des moins. Pourriez vous m'expliquer comment on calcule la primitive? merci

Oui, quand j'aurais remplacé les _ par des -

Vu la clarté de tes questions, je préfère te demander au préalable de quelle fonction dois-tu chercher la primitive ? (Vu qu'on en est à déjà 2 expressions différentes de f(x). )

Bonjour il s'agit en fait d'un autre problème : f(x)= x(1-lnx) dont je veux calculer la primitive
Merci

D'accord, merci de préciser.

Là, il faut faire une intégration par parties, je ne sais si tu as vu cela en cours.