Inscription / Connexion Nouveau Sujet
Exprimer l’aire du triangle ANM en fonction de x.
Bonjour,
pouvez-vous m'aider à résoudre cet exercice?
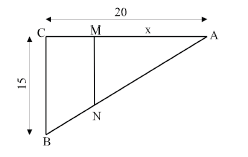
Les données numériques sont en centimètres.
1. Exprimer l'aire du triangle ANM en fonction de x.
2. Quelle est la nature du quadrilatère CMNB ?
3. Exprimer l'aire de ce quadrilatère CMNB en fonction de x.
4. Quelle est la valeur de x pour que le triangle ANM et le quadrilatère CMNB aient la même aire ?
5. Quelle est la valeur de cette aire ?
Pour le 1, je pensais utiliser le théorème de Pythagore pour trouver AB, puis la réciproque pour vérifier si le triangle et rectangle et prendre alors la hauteur AB et le côté AC / 2 pour calculer l'aire ( je ne sais pas si ça peut être utile vu qu'on doit trouver l'aire de AMN en réalité...)
Mais je ne sais pas si je peux le faire étant donné qu'on ne sait pas si le triangle est rectangle : a-t-on le droit d'utiliser le théorème de Pythagore ou non?
Je pensais aussi essayer par Thalès, mais pareil : on n'a pas les informations sur le parallélisme!
Merci beaucoup par avance pour votre aide.
Bonjour,
tu dois avoir quelque part des renseignements sur le triangle ABC et sur les droites (MN) et (BC)...cherche bien
Bonjour ,
bien qu'il n'y ait aucune information précise , la figure ne laisse aucun doute : le triangle ABC est rectangle en C et MN // CB.
Donc tu peux utiliser Thalès .Sinon ce n'est pas possible de raisonner .
Cordialement
Merci pour ta réponse!
Je prépare un concours (le crpe). Donc selon toi, si le jour du concours il y a un exercice de ce type c'est-à-dire aucune précision sur le fait que le triangle est rectangle et sur le parallélisme on peut en déduire automatiquement ces données?
Je pensais calculer AB avec le théorème de Pythagore puis en déduire AN. Mais tu me conseilles plutôt Thalès?
Tilk_11 j'ai posté l'exercice tel qu'il est, il n'y aucune information supplémentaire! :/
merci pour vos réponses!
Tu ne peux utiliser Pythagore que si le triangle est rectangle . Et tu ne peux utiliser la réciproque que si tu connais les 3 côtés .
Mais dans cet exercice tu n'as besoin que de Thalès .
Merci.
ah mince, d'accord, j'avais commencé avec Pythagore.
Je reprends avec Thalès alors.
Est-ce que mon début de calcul est juste?
AM/AC = AN/AB = MN/BC
J'ai fait:
AM/AC = MN/BC
x/20 = MN/15
MN = 3/4x
Par contre, pour calculer l'aire (b*h/2), je peux appliquer la formule au triangle AMN sans savoir s'il est rectangle et prendre MN comme hauteur tout de même?
Merci d'avance!
C'est juste mais tu peux faire plus court et plus facile en partant de ce qu'on te demande (ou de ce que tu veux) .
Pour exprimer l'aire de ANM , tu as AM , il te manque MN
Donc tu écris les rapports en partant de ce que tu cherches MN / ... = ... / ...
Ainsi tu n'as que 2 rapports à écrire et pas 3 et tu peux ensuite trouver ce que tu cherches directement MN = ...
d'accord, merci!
Donc j'ai le droit d'affirmer ça sans vraiment avoir de preuves? Enfin là étant donné qu'on a rien de plus je ne vois pas comment je pourrais faire sinon!  )
)
ça me fait un peu peur ce genre d'exercice pour le concours, c'est la première fois où je tombe sur un comme ça où il n'y a pas "d'informations de base"!
Pour l'aire, je trouve :
x * 3/4x /2 = 3/8x2 cm2
est-ce que c'est correct?
ça me paraît bizarre de mettre x2 et cm2 côte à côte..
Bonjour.
N'était-il porté sur la figure que les 2 triangles étaient rectangles? Vérifies?
Durant un examen, on peut toujours informer le surveillant du problème.
S'il n'a aucune information sur la nature des 2 triangles, le problème devient inextricable, l'aire du dit triangle ne va pas dépendre uniquement du coté AM (=x) mais aussi des 2 autres côtés AN et MN.
Si on suppose seulement que BC // MN , on ne pourra qu'utiliser Thales, ce qui est insuffisant on ne pourra plus exprimer AB et MN en fonction de x ni la longueur de BC, . Si ABC est reanglgle en A, alors
fm_31
Tu précises simplement : le triangle ANM étant rectangle , ..
en M. mais ceci implique que ABC est rectangle en A si l'on suppose BC//MN.
Si les triangles ANC et AMN sont rectangles respectivement rectangles en C et M, on calcule AB (Pythagore) puis exprimer AN en fonction de x (Thales), puis MN en fonction x (Pythagore) et enfin l'aire du triangle AMN.
@dafidou
C'est bien ce tu comptais faire.
Erreur de frappe
Si les triangles ABC et AMN sont rectangles respectivement rectangles en C et M, on calcule AB (Pythagore) puis exprimer AN en fonction de x (Thales), puis MN en fonction x (Pythagore) et enfin l'aire du triangle AMN.
Merci beaucoup delta pour tes précisions!
Il n'y a en effet aucune autre information pour cet exercice!
Je reprends alors l'exercice depuis le début! Il m'aura donné du fil à retordre celui-là!
J'y retourne! 
Bonjour,
une méthode un peu plus rapide, et qui me semble utile d'un point de vue théorique.
On suppose que (MN) (CB), sinon on ne peut rien dire.
(CB), sinon on ne peut rien dire.
Alors le triangle (AMN) est l'image du triangle (ACB) par une homothétie de centre A et de rapport r=x/20. (une similitude de rapport r=x/20 suffirait).
L'aire de (AMN) est égale à r², soit(x/20)², fois l'aire de (ABC).
À retenir « les aires sont entre elles comme le carré des longueurs » Galilée
Verdurin ton idée est intéressante, merci!
Il est possible d'avancer ces propos sans plus de preuves? seulement en supposant le parallélisme?
Donc la réponse serait ce que tu dis : (x/20)2 pour l'aire de AMN?
Merci Verdurin, j'ai fait la question 1 avec ta méthode.
Est-ce que quelqu'un peut m'aider pour les autres questions:
2) Le quadrilatère CMNB est un trapèze rectangle en M et en C car on suppose que (MN)//(CB).
Est-ce que ça suffit pour prouver la nature de ce quadrilatère?
3) Si je fais la méthode proposée par Verdurin, j'en déduis que l'aire du quadrilatère CMNB en fonction de x est:
Aire ABC (r) - Aire AMN (r2)
soit:
r - r2
r =(15*20)=300
r2= 300*1/2=150 (*1/2 car AMN est une réduction d'ABC)
Donc Aire CMNB = 300 - 150 =150 cm2
Pour les deux autres questions je suis un peu perdue aussi..
Merci d'avance!
Si on se concentre sur les questions , les solutions sont quand même assez simples .
1- aire du triangle ANM = MN . AM / 2
MN / 15 = x / 20 soit MN = 3 x / 4 (déjà trouvé)
aire = 3x²/4
2- nature du quadrilatère CMNB ? trapèze rectangle
3- aire quadrilatère CMNB = aire ABC - aire AMN = 20.15/2 -3x/4 = 150 - 3x/4
4- si AMN et CMNB ont même aire alors aire AMN = 150/2=3x/4 soit x = 100
5- aire AMN = 300/4 = 75
et c'est tout (pas besoin de Pythagore).
J'aurais préféré que ce soit toi qui trouve les réponses car ce n'était pas trop compliqué si on reste concentré sur les questions . Mais si tu as compris ...
Si tu peux retenir que pour appliquer Thalès , le plus simple c'est de commencer par ce qu'on cherche pour écrire les rapports , c'est encore mieux .
oui je vais tâcher de m'en souvenir!
merci!
je referai l'exercice plus tard pour vérifier si j'ai tout assimilé 
Bonjour.
Si l'on suppose que ABC est rectangle en C et que MN//BC alors AMN est rectangle en M. On peut donc applquer le théorème de Pythagore dans AMN. La méthode que j'avais préconisée et peut-être que voulait adopter dafidou est valable sauf que et non
. Mais ce qu'a fait fm_31 est nettement plus rapide.
Bonjour à tous et à toutes,
j'ai demandé des informations afin de savoir s'il n'y avait pas des erreurs dans l'énoncé (oubli de la mention du parallélisme, triangles rectangles) au cas où. Donc j'attends de voir s'il y a bien ou non des erreurs et je vous tiendrai informés dès que j'en sais plus.
Merci pour votre aide!
Bonne journée!
Je ne pense pas qu'on puisse parler d'erreurs dans l'énoncé . Simplement un énoncé et/ou figure incomplets ou à interpréter (volontairement ou pas). Cela peut arriver en cours . C'est heureusement extrêmement rare en examen .
Mais je reconnais que cela peut jeter un trouble qu'il faut surmonter par la maîtrise du sujet en voyant rapidement que sans droites parallèles on ne peut appliquer Thalès et sans angle droit on ne peut exprimer l'aire .
Et pour Thalès , je le redis parce que cela me parait important , partir pour établir les rapports , de ce qu'on cherche . Cela évite des calculs inutiles .
Bonjour fm_31! Et bonjour à tous les autres!
si par hasard tu es encore là..?
Alors j'ai eu l'information : en effet, il manquait les précisions suivantes :
- les triangles ABC et AMN sont des triangles rectangles respectivement en A et en C
- les droites (BC) et (MN) sont parallèles
J'aurais une autre question, si quelqu'un peut m'aider (ou fm_31 si tu vois mon message  )
)
Alors, je me demandais si, comme en question 1, on trouve:
" aire = 3x²/4 "
si en question 3 et 4 il ne manquerait pas le carré de x?
"3- aire quadrilatère CMNB = aire ABC - aire AMN = 20.15/2 -3x/4 = 150 - 3x/4
4- si AMN et CMNB ont même aire alors aire AMN = 150/2=3x/4 soit x = 100"
Du coup pour la question 3 on aurait Aire CMNB = 150 - 3/4x2
et pour la question 4 x2= 100 donc x=V100 (racine carré de 100) donc x= 10 cm2
Y aurait-il quelqu'un qui pourrait m'aider?
Merci d'avance!
Eh bien! mon niveau doit être regrettable alors... honte à moi!
Mais je suis là pour apprendre 
Merci quand même pour ta réponse bien que ça ne m'ait pas aidé :/
Bonjour delta-B,
merci de me venir en aide.
En fait j'ai bien vu que fm_31 m'a bien indiqué les réponses mais je me demandais si quand on reprend l'aire de AMN dans les questions 3 et 4 pour faire les calculs si il ne faudrait pas mettre 3x2/4 au lieu de 3x/4. Car on exprime l'aire en carré. C'est juste ça qui m'embête :/
Bonjour.
Tu as raison de te poser car effectivement, il a des erreurs de calculs.
Même la formule donnant l'aire du triangle AMN est fausse, ce n'est ni 3x/4 ni 3x2/4 mais 3x2/8.
Si M est confondu avec C, alors aire(AMN)=aire(ABC)=(20 15)/2=150 cm2 mais 3x/4=(3
15)/2=150 cm2 mais 3x/4=(3 20)/4=15 et 3x/4 n'a pas la diemsion d'une aire, 3x2/4=(3
20)/4=15 et 3x/4 n'a pas la diemsion d'une aire, 3x2/4=(3 202)4=3
202)4=3 20
20 5=300 cm2
5=300 cm2 aire(ABC).
aire(ABC).
Si l'on reprend depuis le début, le théorème de Thalès (ou la similitude des 2 triangles AMN et ABC) : AM/AC=MN/BC soit MN=(AM BC)AC=3x/4 et aire(AMN)=(AM
BC)AC=3x/4 et aire(AMN)=(AM MN)/2=(x
MN)/2=(x (3x/4))2=3x
(3x/4))2=3x
2/8.
Avec cette correction,tu peux continuer toute seule, le quadrilatère MNBC est un trapèze rectangle dont l'aire vaut ((MN+BC) CM))/2=(15+3x/4)
CM))/2=(15+3x/4) (20-x)/2=150-3x2/8 (à vérifier)
(20-x)/2=150-3x2/8 (à vérifier)


 géométrie en post-bac
géométrie en post-bac