Inscription / Connexion Nouveau Sujet
Exrcice de géométrie: besoin d aide merci.
Salut !
J'ai besion de votre aide pour cet exercice de géometrie ! Merci d'avance !!
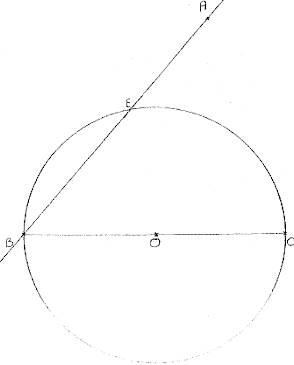
On considère un cercle C de centre O et un de rayon 5 cm.
- [BC] est diamètre de C. On construit le point A tel que l'angle CBA = 50° et BA = 11 cm.
- (BA) coupe C en E et (AC) coupe C en F. H est le point d'intersection des droites (EC) et (BF).
1) Quelle est la nature des triangles BEC et BFC ? Justifier.
Montrer que (AH) perpendiculaire à (BC).
2) Quelle est la mesure de l'angle BCE ? En déduire la mesure de l'angle EOB.
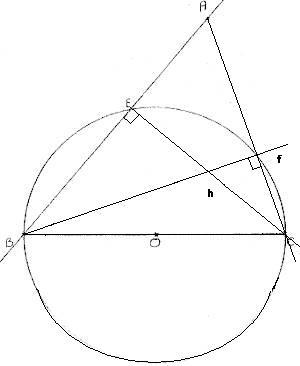
3) La tangente au cercle C en E et la tangente à C en B se coupent en K.
a) Quelle est la nature des triangles KEO et KBO ? Pourquoi ?
b) Calculer EK en fonction de OK puis KB en fontion de OK. En déduire que BKE est isocèle en K.
c) Que représente (OK) pour le segment [BE] ? Justifier.
4) La parallèle à (OE) passant par C coupe (BA) en S.
Montrer que S est le symétrique de B par rapport à E. Justifier.
Salut
un début
BEC et BFC sont des triangles rectangles respectivement en E et F
parce qu'ils sont inscrit dans un cercle et qu'un de leurs côtés est un diamètre
°
bon j'ai pas beaucoup de temps je te mets sur la voix.
Théoreme: Si un triangles est placé dans un demi cercle et que le diametre correspond a son hypoténuse, alors ce triangle est rectangle.
Donc en fait les deux triangles sont rectangle, ensuite pour prouver ke AH est une hauteur (perpendiculaire a BC , ben tu sais ke si BEC et BFC sont rectangle, EC perpedendiculaire a AB et BF perpendiculaire a AC donc c des hauteurs du triangle, H est l'orthocentre, donc AH coupe BC perpendiculairement.
Bon courage pour la suite si tarrive pas je t'aide ce soir. @+
ton exercice est pas bien compliqué, Lopez et moi t'avons fait la moitié, la suite est aussi simple, ce n'est que des applications de formules.
Bonne chance pour la suite...
un conseil fait ton dessin dans son intégralité tu verra, une bonne compréhension du problème provient de sa figure, si tu suis ce conseil expose le sur ce topic ca incitera peut etre d'autre personne à t'aider.
Pour la 4) si tu veux je peut te donner un ptit coupde pousse. Pour montrer que S est le symétrique de B par rapport a E, tu utilise les longeurs, tu sai que:
OB = OC (rayons du cercle)
tu sais aussi que la parallele à (OE) passant par C (BA) en S
or E est sur (BA)
synthese ou conclusion:
(OE) // (CS)
OB étant égal a OE et OC (B, E, et C sur le cercle)
On déduit que S est le symétrique de B par rapport E.
Bon j'espère que tu m'a compris lol parce que j'ai fait ca à la va vite et ma démonstration après relecture n'est pas top lol. Enfin le principal c'est que tu comprenne après tu fait ta sauce.Bonne chance @+
je vous remerci Lopez et infophile vous mavé bien aidé !!
C sympa
Y'a pas d'quoi! Sur l'ile le secret c'est l'entraide mais il ne faut pas en abuser! Si tu as un problème en maths consulte d'abord ton cours (c'est la source qui te sera la plus utile puisque cest ton prof qui te fourni le travail), si vraiment tu ne trouve pas tu peux poster sur le forum. D'ailleurs jte le dis en passant il m'est arrivé une ou deux fois de poster moi aussi sur l'île 
Sur ce bonne continuation 
P.S: Si tu poste souvent ici tu t'apercevra que niveau seconde il y a le mmodérateur Nightmare qui a notre age qui est très très doué. Enfin tu vérifiera par toi même 
@peluche
c'est bon je vien de completer la figure. Et je comprend mieu la !!
Je narive tjs pas a la question 3). Pouver vous maider ? Merci
Salut,
la 3) les 2 triangles KEO et KBO sont rectangles respectivement en E et B
parce que la tangente à un cercle est perpendiculaire au rayon en ce point
donc (KB) est perpendiculaire à (OB)
de même (KE) est perpendiculaire à (EO)
pour compléter ton dessin :
tu traces la droite perpendiculaire en E à (EO)
et la droite perpendiculaire en B à (OB)
ces 2 droites se coupent en K
la suite c'est pythagore et tu dois trouver que le triangle KBE est isocèle en K
(OK) est la médiatrice de [BE]
Annuler
connectez vous