Inscription / Connexion Nouveau Sujet
Ficelle et triangle rectangle.
Bonsoir ,
Merci d'avance.
Une ficelle , d'une longueur L en cm , est fixée à ses extrémités par des clous A et B distants de 65 cm.

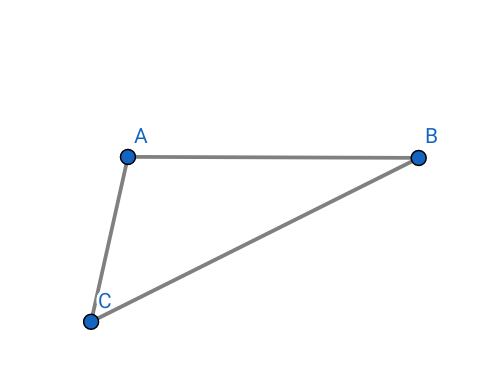
Est -il est possible de tendre la ficelle de façon que le triangle ACB soit rectangle en C.
Alors j'ai pensé à Pythagore :
Pour que ACB soit rectangle en C , il suffit que AB²=AC²+BC²
Que ne comprenez-vous pas ?
Il faut bien une condition sur L pour savoir si c'est possible
Si et
sont les longueurs des côtés on a
.
Écrivez aussi le théorème de Pythagore
Non
Une ficelle, d'une longueur L en cm,
AB est la longueur de l'hypoténuse du triangle s'il existe
Non Si L<65 il n'y a pas de triangle
un côté est toujours plus petit que la somme des deux autres et plus grand que leur différence
pour 65 les points sont alignés
L est la longueur de la ficelle que vous avez et AB est la distance entre les points où sont attachées les extrémités d'icelle.
On peut avoir L= 80 cm par exemple
Commençons par cela si vous voulez on généralisera ensuite le problème.
Exercice Une ficelle de 80 cm est attachée à deux pieux distants de 65 cm.
Peut-on trouver un point C pour que le triangle ABC soit rectangle en C.
Appliquez Pythagore en utilisant ces valeurs numériques.
Soit a=AC et b=BC les deux autres côtés formés par la ficelle et c=AB.
ABC est rectangle en C si
c²=a²+b² <==> 65²=a²+b² <==> 4225=a²+b²
C'est là que je bloque.
Oui , a+b+65=80
Donc a+b-15=0
Donc a=15-b
=> b²+a²=65²
b²+(15-b)²=65²
b²+15²-30b+b²-65²=0
2b²-30b-4000=0
∆=32900
√∆=10√(329)
et
Une distance étant toujours positives , on retiendra b2.
Pour que ABC soit rectangle en C on peut tendre BC de cm
salut
Vous avez oublié que
puis
Oui , a+b+65=80
a+b=80
Donc a=80-b
=> b²+a²=65²
b²+(80-b)²=65²
b²+80²-160 b+b²-65²=0
2b²-160b+2175=0
∆=8200
√∆=10√82
et
Oui donc il existe deux positions pour que le triangle ABC soit rectangle en C
Maintenant au lieu de 80 on a L d'où
Bonjour,
Le 82 sous le radical ne doit pas non plus être conservé, car le discriminant dépend de L .
En reprenant ce que vous aviez déjà effectué dans le poste équation et inéquation
Résoudre l'inéquation
une remarque : il y a toujours deux solutions car comme dans le sujet ![]() Aire de deux triangles. la figure est symétrique par rapport à la médiatrice du segment [AB] ...
Aire de deux triangles. la figure est symétrique par rapport à la médiatrice du segment [AB] ...
pourquoi une inégalité ?
Soit a=AC et b=BC les deux autres côtés formés par la ficelle et c=AB.
ABC est rectangle en C si et seulement si
c²=a²+b² <==> 65²=a²+b² <==> 4225=a²+b²
a + b = L
Ok ,
Soit a=AC , b=BC.
ABC est rectangle en C si et seulement si :
65²=a²+b² <==> 4225=a²+b².
Or a+b=L
Donc b=L-a
==> a²+(L-a)²=4225 <==> a²+L²-2aL+a²=4225
Donc 2a²+L(L-2a)-4225=0
L est un paramètre et a est l'inconnue de ton équation qui est donc un trinome du second degré d'inconnue a ...
à quelle condition auras-tu des solutions ? (relis bien la question de l'énoncé)
C'est largement insuffisant
Vous savez bien résoudre une équation du second degré.
Pour qu'il existe C, l'équation doit avoir des solutions. À quelle condition ?
Oui , mon problème est que je ne comprends plus rien depuis 10:18..
Je remplace 80 par L est c'est faux ..
Je vous avais proposé un exemple numérique pour voir comment on pouvait résoudre le problème.
Pouvait-on trouver la longueur d'un côté pour que le triangle ABC soit rectangle en C ?
Maintenant la longueur de la corde est L. On sait que L doit être d'au moins 65 si l'on veut déjà construire un
triangle et d'autre part pas trop grand non plus pour que le triangle puisse être rectangle.
Le point C doit d'ailleurs appartenir au cercle de diamètre [AB]
Pour le déterminer on a deux relations et
De ceci il vient
En développant on a
Pour que C existe il faut que cette équation ait des solutions, fussent-elles égales donc on en déduit que
Que vaut ? Pour quelles valeurs de L icelui est positif.
Écrivez et résolvez l'inéquation d'inconnue L
On sait que ∆= b²-4ac
Cette équation est un peu bizarre quand même ..
Si j'avais L²-2L -4225 =0
J'aurais tout de suite vu que :
∆=(-2)²-4×1×(-4225).
Mais là : 2a²-2La+L²-4225=0
Je ne vois pas grand chose.
On a 2a²-2La+L²-4225=0
Équivaut à
L²+a(2a-2L)-4225=0
Puis là je ne vois plus quoi faire.
Si au lieu d'avoir appelé les longueurs des côtés et
vous les aviez appelées
et
alors l'équation aurait été
Dans le calcul de vous n'auriez pas demandé où sont les
?
est l'inconnue. Le problème ici est qu'il y a des homonymes
le de
et le
longueur d'un côté
Pour que l'équation ait des racines oui doit appartenir à
mais si l'on revient aux côtés du triangle alors la longueur de la ficelle doit être comprise entre 65 exclu et
Vous pouvez maintenant préciser la position de C en calculant et
Ok ,
L²+a(2a-2L)-4225=0
Si L=65 , 65²+2a²-2a×65-4225=0
2a(a-1)×65=0
2a(65a-65)=0
2a²×65-65×2a=0
2a²×65=65×2a
2a×65=65×2
a=(65×2)/2×65
a=1
????
Pourquoi ce changement dans la résolution d'une équation du second degré ?
On pourra construire un triangle rectangle si
Un côté de l'angle droit aura comme longueur et le second
ou a_2
On peut remarquer que pour le point C appartient à la médiatrice de [AB]
OK.
On peut remarquer que pour
Je ne vois toujours pas comment vous avez fait pour remarquer celà.
On pourra construire un triangle rectangle si
Un côté de l'angle droit aura comme longueur
On peut remarquer que pour
On peut donc tendre la ficelle en AC d'une distance
On pourra construire un triangle rectangle si
Un côté de l'angle droit aura comme longueur
On peut remarquer que pour
On peut donc tendre la ficelle en AC d'une distance
Merci beaucoup

Vous avez dit à un moment que par conséquent pour
on a donc pour solution de l'équation Ce qui signifie aussi que AC=BC
donc le point C se trouve sur la médiatrice de [AB]
Vous avez bien fait de corriger c'est bien qu'il fallait lire et non
Si alors il existe au moins un point C tel que le triangle ABC soit rectangle en C
Les deux points sont symétriques par rapport à la médiatrice de [AB]
De rien