Inscription / Connexion Nouveau Sujet
figures complexes
Bonsoir à tous
j'ai su faire ma figure mais je ne peux vous la montrer problème de scanne mais je ne sais pas démontrer le A B Cje n'arrive pas à expliquer quelqu'un peut'il m'aider ?
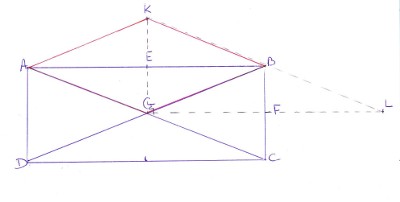
ABCD est un rectangle de centre G. On appelle E le milieu de[AB], F le milieu de [BC}, Kle symétrique de G par rapport à E et L le symétrique de G par rapport à F.
A/ Démontre que le quadrilatère AGBK est un losange.
B/ Démontre que B est le milieu du segment [KL].
C/ Démontre que GKL est un triangle rectangle en G.
Merci d'avance
édit Océane : niveau modifié
Bonsoir Corinne..tte . Donc tu n'as rien fait ...à peine le dessin ...
Qu'est-ce que tu connais d'un losange? comment pourrait-on montrer que AGBK est un losange ? quelles propriétés faudrait-il employer ?
bonjour
merci lolo pour ton shéma oui j'ai le même donc c'est bon et pour répondre aux questions de jacqlouis est bien je sais que :
un quadrilatère qui a ses diagonales perpendiculaires qui se coupent en leur milieu est un losange
un quadriltère qui a ses diagonales perpendiculaires et de même longueur est un losange
mais peut être en a t'il d'autres, en plus mon prof veut qu'on démontre d'une certaine façon genre je sais que ,alors,donc et c'est ca que je ne sais pas formuler
merci à vous
Bonjour Corinnette . C'est précisement pour t'aider à répondre à ton prof, et à rédiger ton devoir , que je t'ai posé ces questions ...
Je sais que le point E est le milieu de AD
Je sais que E est également le milieu de GK puisque G est symétrique de K...
Je sais aussi que EK est perpendiculaire à AD
...alors le quadrilatère AKBG ...
DONC .....
olala si je comprends bien je dois tous à chaque fois je sais que ................
ensuite je note alors le quaedrilatère AGBK est un losange donc ????????
désolé j'ai beaucoup de mal
en plus les autres questions me posent problèmes j'ai fait des recherches sur les propriétés mais dur de rediger
... alors le quadrilatère AGBK a ses deux diagonales perpendiculaires, qui se coupent en leur lieu .
Donc AGBK est un losange .
Question 2. Puisque GB est égal à KB (cotés du losange)
et puisque GB est égal à BL (symétrie de L par rapport à G )
alors KB = BL, et B est le milieu de KL .
merci beaucoup jacqlouis pour ton aide et pour la 3 on demande de démontrer que GKL est un triangle rectangle en G mes recherches me donnent de calculer le théorème de pythagore pour démontrer mais on ne l'a pas encore etudier en classe comment puis je démontrer alors?
Ce n'est pas dans Internet qu'il faut chercher les réponses ... C'est dans ton cours, et dans ta tête avec tout ce que tu as appris !....
Cherche plutôt dans les propriétés du rectangle ABCD : ses diagogonale ne sont pas perpendiculaires ?...
(je m'absente jusqu'à 16h00)
désolé je vois que G est le milieu des mes diagonales et qu'il est aussi le point qui forme l'angle droit dans mon triangle rectangle mais je sais pas expliquer
K est le symétrie de G par rapport à E
L est le symétrie de G par rapport à F après je sais pas ?????????????? 
Les droites GK et GL sont perpendiculaires aux cotés du rectangle, donc elles sont perpendiculaires entre elles , donc l'angle G est un angle droit ...
ok je te remercie beaucoup pour ton aide jacqlouis c'est plus clair pour moi maintenant bonne soirée