Inscription / Connexion Nouveau Sujet
Fonction
Bonjour c'est pour un DM de mathématiques et je n'y arrive pas. Le problème à étudié est: une fourmi alléchée par l'odeur du sucre mais paresseuse se demande quel est le plus court chemin pour atteindre l'objet de sa convoitise. En quel point point N, de l'arrête [A'B'], la fourmi doit-elle passer pour que le trajet M-N-S soit le plus court possible? Le cube à pour arrête 3cm, S est le milieu de [A'D'] et BM=1cm.
1. a. Quel est le plus court chemin des deux trajets M-B'-S et M-A'-S?
b. On pose x=B'N, en cm. À quel intervalle appartient x?
c. Quelle est la nature du triangle MB'N?
Exprimer la longueur MN en fonction de x.
d. Exprimer A'N et NS en fonction de x puis la longueur L(x) du trajet M-N-S.
e. En quel point la fourmi doit-elle traverser l'arrête [A'B'] ?
2. a. Tracer en vraie grandeur le patron du cube ci-contre et y placer les sommets du cube et le point M. Tracer le plus court chemin de M à S.
b. Calculer la longueur B'N correspondante. Commenter ce résultat.
Je ne comprend rien de rien pour la question 1a. Comment on arrive à faire? Et la b comment on trouve?
Qui peut m'expliquer s'il vous plait
bonjour
En quel point point N, de l'arrête [A'B'], la fourmi doit-elle passer pour que le trajet M-N-S soit le plus court possible? Le cube à pour arrête 3cm, S est le milieu de [A'D'] et BM=1cm.
je suppose que tu as une photo, croquis .... poste la ou le
Bonjour c'est pour un DM de mathématiques et je n'y arrive pas. Le problème à étudié est: une fourmi alléchée par l'odeur du sucre mais paresseuse se demande quel est le plus court chemin pour atteindre l'objet de sa convoitise. En quel point point N, de l'arrête [A'B'], la fourmi doit-elle passer pour que le trajet M-N-S soit le plus court possible? Le cube à pour arrête 3cm, S est le milieu de [A'D'] et BM=1cm.
1. a. Quel est le plus court chemin des deux trajets M-B'-S et M-A'-S? Je dois m'aider de quoi pour savoir qu'elle chemin prendre?
b. On pose x=B'N, en cm. À quel intervalle appartient x? Comment on trouve une intervalle en utilisant un carré?
c. Quelle est la nature du triangle MB'N?
Exprimer la longueur MN en fonction de x.
Je sais que la nature est un triangle isocèle rectangle mais comment on exprime une longueur en fonction de x?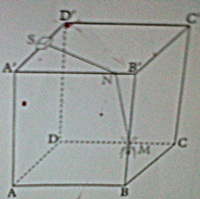
*** message déplacé ***
* Glapion > le multi-post n'est pas toléré sur le forum ! *
Lidvine
ce n'est pas la peine de faire un double-post.
fais un tour : ![]() La fourmi paresseuse géométrie
La fourmi paresseuse géométrie
Ok, l'image est passée.
1) Ce n'est pas difficile. On te demande lequel des 2 chemins est le plus court.
Trajet M-B'-S = MB' + B'S (la longueur B'S tu peux facilement le calculer par Pythagore)
Idem pour M-A'-S = MA'+A'S (la longueur MA' facilement calculable par Pythagore aussi)
A toi.
Ah d'accord merci j'ai compris mais comment on fais pour trouver une intervalle sur un carré on se sert aussi de pythagore?
On pose x=B'N, en cm. À quel intervalle appartient x ?
On te demande l'intervalle.
En d'autres termes, quelles sont les valeurs que peuvent prendre ta longueur x ?
Pour la question c j'ai trouver la nature mais ils veulent que j'exprime la longueur MN en fonction de x..ça veut dire quoi?
La d j'ai fais A'N+NS (en utilisant pythagore) mais le truc qui me gène c'est qu'ils disent en fonction de x
c) Tu te places sur le mauvais triangle là !! C'est sur le triangle MB'N où tu dois faire tes calculs...
Appliques tout simplement Pythagore sur ce triangle.
Lorsqu'on te dit "en fonction de x", c'est que dans ton expression finale doit y figurer du"x"...
On me donne l'intervalle?
x appartient au segment [A'B'] !!
Donc x est forcément compris entre .... et ....
Et donc l'intervalle recherchée est ... ??
Non, un intervalle doit toujours être compris entre 2 valeurs !!!
x doit donc être compris entre ..... et ......
On te demande une valeur !!! Pas un point !!!
La longueur A'B' tu la connais c'est 3.
x se balade sur ce segment, donc x doit être compris entre cb et cb ??


