Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction ExponentielleTopics traitant de Fonction Exponentielle [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

fonction

Posté par
xofnxksd 22-12-22 à 20:58

Bonjour,
Je bloque sur un exercice et j'aimerai bien avoir de l'aide.

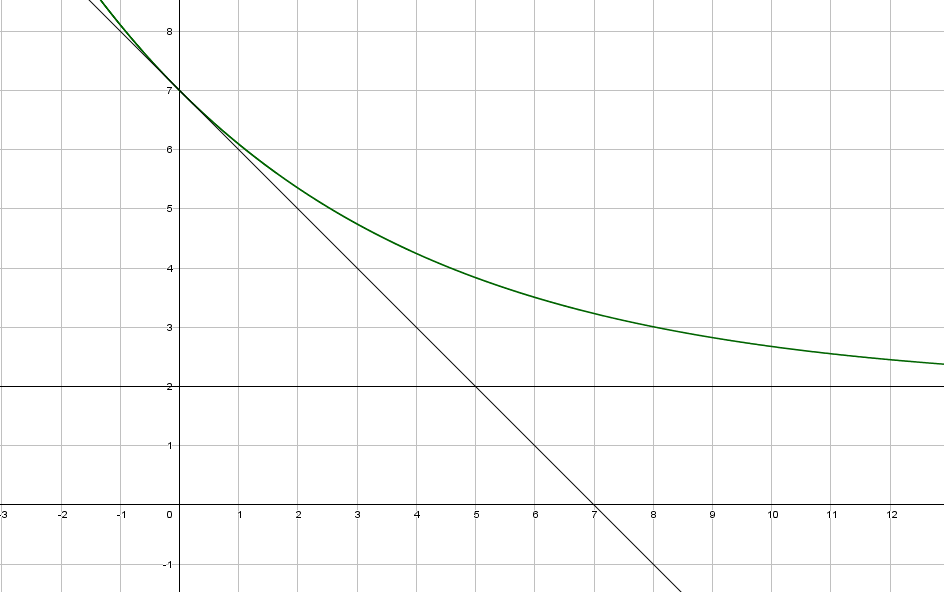
la fonction f est définie sur , f(x)=aebx+c
déterminer l'expression de f sachant que f '(0)=-1 et que Cf passe par A(0;7) et qu'elle admet une asymptote horizontale d'équation y=2 au voisinage de +


Merci d'avance !

Posté par
heklare : fonction 22-12-22 à 21:08

Bonsoir

Que proposez-vous ?
Qu'est-ce qui vous gêne ?

Posté par
xofnxksdre : fonction 22-12-22 à 21:12

J'ai seulement calculé la f '(x) qui donne abebx
mais je ne sais pas comment continué

Posté par
heklare : fonction 22-12-22 à 21:23

Vous avez f'(0)=1 traduisez puisque vous avez calculé f'(x).
Utilisez aussi la donnée, la courbe passe par A.
Cela vous donnera un système de 2 équations à résoudre.

Posté par
xofnxksdre : fonction 22-12-22 à 21:31

excusez-moi je n'ai pas compris et f'(0)= -1
j'ai fais ca mais je ne sais pas si c'est ce qu'il faut faire :
f'(0)=abeb0
donc a=-1/b
b=-1/a

Posté par
heklare : fonction 22-12-22 à 21:37

Il y a encore une autre équation à écrire.

Avez-vous des renseignements sur a ?

Posté par
heklare : fonction 22-12-22 à 21:39

D'accord

on a bien ab=-1

Écrivez que la courbe passe par A.

Posté par
xofnxksdre : fonction 22-12-22 à 21:41

ah oui a=2 donc
f'(0)= 2*(-1/2)*e(-1/2)*0=-1

Posté par
heklare : fonction 22-12-22 à 21:48

Comment avez-vous trouvé 2 ?

Passe par A f(0)= ?

Comment va se traduire l'asymptote horizontale y=2

Posté par
xofnxksdre : fonction 22-12-22 à 21:52

j'ai remplace a par 2 mais il faut le démontrer  et je ne vois pas comment utiliser A(0;7)

Posté par
heklare : fonction 22-12-22 à 21:57

Un point appartient à une courbe si et seulement si ses coordonnées vérifient l'équation de la courbe.

M (x , y) \in \mathcal{C}\iff  M( x, f(x))

Posté par
xofnxksdre : fonction 22-12-22 à 22:02

mais on ne peut pas calculé f(x) car nous n'avons pas c ?

Posté par
heklare : fonction 22-12-22 à 22:05

Il y a encore une hypothèse que vous n'avez pas utilisée,  
l'asymptote

Que vaut f(0) ?

Posté par
xofnxksdre : fonction 22-12-22 à 22:11

mais c nous est pas donné je ne vois pas comment faire

Posté par
heklare : fonction 22-12-22 à 22:18

Résumons

f'(0)=-1  d'où ab=-1

passe par A d'où  a\,\text{e}^{b\times 0}+c=7

y=2  est asymptote au voisinage de +\infty  d'où

C'est ici que l'on a besoin de renseignements supplémentaires sur a   ou il faut supposer  a>0

après on peut résoudre le système formé par les trois équations

Posté par
xofnxksdre : fonction 22-12-22 à 22:27

ah comme aeb*0+c=7

eb*0=1 et que l'asymptote est au voisinage de + on deduit que a =1 et c=6 car
1*1+6=7
?

Posté par
heklare : fonction 22-12-22 à 22:33

Pour l'instant, on a

ab=-1

a+c=7

reste l'asymptote, mais vous ne dites pas comment vous l'utilisez.

Si a<0 on ne peut avoir une asymptote horizontale

La réponse donnera c et ensuite les deux autres

Posté par
xofnxksdre : fonction 22-12-22 à 22:40

pour avoir une asymptote horizontale a>0donc a =1 pour  que 1*(-1)=-1
et a+c=7 donc a-7=-c    et 1-7=-6        c=6

Posté par
heklare : fonction 22-12-22 à 22:45

Non on a une asymptote horizontale y=\ell ,\,( \ell \in \R) au voisinage de +\infty

si \displaystyle \lim_{x\to +\infty} f(x)=\ell

Écrivez donc la limite de f en +\infty

Posté par
xofnxksdre : fonction 22-12-22 à 22:57

lim f(x)=aebx+c =+
x+

car la fonction ex est croissante sur et a>0

Posté par
heklare : fonction 22-12-22 à 23:06

C'est là qu'intervient la nécessité de a>0

ainsi comme ab=-1  on a, alors b<0 et ainsi

\displaystyle \lim_{x\to+\infty}a\,\text{e}^{bx}=\dots $ et $ \lim_{x\to +\infty}f(x)= \dots

Posté par
xofnxksdre : fonction 22-12-22 à 23:10

lim aebx=+
x+

et

lim f(x)=+
x+

Posté par
heklare : fonction 22-12-22 à 23:13

Non, justement \text{e}^{-x} tend vers 0 quand x tend vers +\infty

Posté par
xofnxksdre : fonction 22-12-22 à 23:21

ahh oui c'est vrai excusez moi donc lim aebx=0
                                                                                 x+

Posté par
heklare : fonction 22-12-22 à 23:25

On a ainsi obtenu :

\displaystyle \lim_{x\to+\infty}a\,\text{e}^{bx}=0 $ et $ \lim_{x\to +\infty}f(x)= \dots

Posté par
xofnxksdre : fonction 22-12-22 à 23:31

par somme lim f(x)=aebx+c= l*l'
                            x+

Posté par
xofnxksdre : fonction 22-12-22 à 23:31

l+l'

Posté par
heklare : fonction 22-12-22 à 23:34


Par addition on a ceci

\displaystyle \lim_{x\to +\infty}f(x)=0+c


On sait que cette limite vaut

par conséquent c=

Posté par
xofnxksdre : fonction 22-12-22 à 23:42

cette limite vaut +                  par conséquent c=7

Posté par
heklare : fonction 22-12-22 à 23:46

Non, faites attention. Ce ne peut être +\infty   car on aurait alors c=+\infty, ce qui est impossible et adieu l'asymptote !

Posté par
xofnxksdre : fonction 22-12-22 à 23:47

ah donc cette limite vaut 7

Posté par
heklare : fonction 22-12-22 à 23:57

Non, l'équation de l'asymptote est y=2

Posté par
xofnxksdre : fonction 22-12-22 à 23:59

la limite vaut 2 ?

Posté par
heklare : fonction 23-12-22 à 00:10

oui, c d'une part et 2 de l'autre donc c=2

Conclusion

\displaystyle  \lim_{x\to +\infty}f(x)=c=2

ce qui implique que a soit strictement positif

on a alors ab=-1 et a+2=7

\begin{cases} a=\\ b=\\c=\end{cases}

f est la fonction définie par f(x)=

Posté par
xofnxksdre : fonction 23-12-22 à 00:14

mais il y a donc plusieurs solutions pour a et b ?

Posté par
heklare : fonction 23-12-22 à 00:20

Non, il n'y a qu'une unique solution.

Posté par
xofnxksdre : fonction 23-12-22 à 00:27

ah
a= 1
b=-1
c=2
c'est ça ?

Posté par
heklare : fonction 23-12-22 à 00:32

Vous croyez que 1+2=7 ?


si a+c=7 et c=2 on a donc a=

Posté par
xofnxksdre : fonction 23-12-22 à 00:40

a=5 si c=2

Posté par
heklare : fonction 23-12-22 à 00:41

Il reste encore b  sachant que ab=-1

Posté par
heklare : fonction 23-12-22 à 00:52

Vous auriez pu conclure.

fonction

Posté par
xofnxksdre : fonction 29-12-22 à 14:01

bonjour, j'ai reflechis sur l'exercice mais je ne comprend toujours pas pouquoi a=5 sachant que ab=-1et pourquoi c =2.
svp pourriez-vous m'éclairer

Posté par
heklare : fonction 29-12-22 à 14:58

Bonjour
Nous avons 3 renseignements pour définir l'expression de f, sachant qu'elle est de la forme f(x)=a\text{e}^{bx}+c

Premier renseignement f'(0)=-1

on dérive donc,  f'(x)=ab\text{e}^{bx}

soit pour x=0,\  f'(0)=ab \boxed{ab=-1}

Deuxième renseignement   la courbe passe par A (0{,}7)

il en résulte f(0)=7, par conséquent a\text{e}^{b\times 0}+c=7

c'est-à-dire \boxed{a+c=7}

Troisième renseignement   La courbe admet une asymptote horizontale d'équation y=2 au voisinage de + \infty. Dire cela signifie que \lim_{x\to +\infty}f(x) =2

On est donc amené à déterminer la limite de f au voisinage de +\infty

\lim_{x\to +\infty}f(x)=\lim_{x\to +\infty} a\text{e} ^{bx}+ \lim_{x\to +\infty }c

\lim_{x\to +\infty} a\text{e} ^bx}= \begin{cases}a\times +\infty& \text{si } b>0\\0&\text{si  }b<0\end{cases} \\ \\

\lim_{x\to +\infty }c = c

Puisque la limite en + \infty est finie et vaut 2, il est nécessaire que b soit strictement négatif,

d'où \lim_{x\to +\infty }f(x)=a\times 0+c \  \boxed {c=2 \ \text{et } b<0}


On a donc à résoudre

\begin{cases} b<0\\  ab=-1\\ a+c=7 \\c=2\\\end{cases}

dans la deuxième ligne, on peut calculer a. , a+2=7 d'où a=5

Dans la première ligne, ab=-1 d'où b=-\dfrac{1}{a} ou encore puisque a=5,\ b=-\dfrac{1}{5}=-0,2

Conclusion du système  

\begin{cases}a-5\\b=-\frac{1}{5}=-0,2\\c=2\end{cases}

Posté par
xofnxksdre : fonction 29-12-22 à 18:43

ohh je vous remercie beaucoup pour le temps consacré a cet exercice je viens de comprendre plus de choses !

Posté par
heklare : fonction 29-12-22 à 18:52

De rien

Il ne faut jamais hésiter à demander des explications
Bonne soirée


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1694 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !