Bonsoir
1)
a)OA étant perpendiculaire au plan ABCD , OA est perpendiculaire ...
b)MN est // AD car AD est // OCB et tout plan passant par cette droite (AD) le coupe suivant une droite (MN) // à cette droite ( BC) donc MN // AD
Je crois que vous avez permuté M (sur OB) et N (sur OC)
Voulez - vous me confirmer que c'est bien le cas
AC² =  64+64 = 8².2  => AC = 82
OB² = OA²+AB² = 8²+8² = 2.8²
OC² = OA²+AC² = 64+2.64 = 3.64  => OC = 8.3
A+

non l'enoncé est bon c'est M sur OC et N sur OB

Re
Donc on a M sur OC et N sur OB
1a)
a)
demontrer que les faces laterales de la pyramide sont des triangles rectangle ?
OA étant perpendiculaire au plan ABCD , OA est perpendiculaire  à AB , à AD => OAB et OAD sont des triangles rectangles; OB est  perpendiculaire  à BC  => OBC est un triangle rectangle ; OD est  perpendiculaire  à DC => ODC est un triangle rectangle.
b)
le quadrilatère AMND est un trapèze rectangle ??
MN est // AD car AD est // OCB et tout plan passant par cette droite (AD) le coupe (OCB) suivant une droite (MN) // à cette droite ( BC) donc MN // AD
AD est perpendiculaire au plan OAB => AD est perpendiculaire à AM
2)
a)
AC² =  64+64 = 8².2  => AC = 8V2  (V = racine)
OB² = OA²+AB² = 8²+8² = 2.8² => OB =8V2
OC² = OB²+BC² = 64.2+64 = 3.64  => OC = 8.V3
Dans le triangle BOC MN est // BC  =>
OM/OC = MN/BC  => MN = 8xV2/(8V3) = x.V(2/3)

AM =  à chercher mais inutile pour chercher l'aire
l'aire du trapèze rectangle (en A) = (AD+MN)*AN/2  ( AN étant la hauteur-  => aire = (8+xV(2/3))*AN/2
et ici ABCD étant le carré ( et non ACBD dans le sens trigonométrique) il y a un souci pour chercher AM ou AN
ce ne serait pas plutôt ON = xV2 ????
A+

Bonjour,

si tu n'as pas permuté M et N c'est que tu as permuté B et C !!

quand on cite un carré ABCD c'est toujours "en tournant autour" :

A B

D C

et seuls les "fantaisistes" parlent de
A B

C D

de plus il manque une info essentielle sur M et N ou sur le plan AMN parce que sans cette info A, M, N et D ne sont même pas dans un même plan !!
et ne peuvent donc pas former quelque "trapèze" que ce soit.

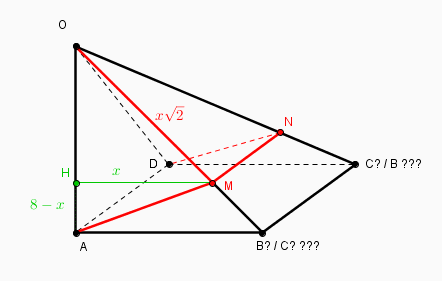
j'en déduis donc qu'il y a une figure avec cet exo, figure dans laquelle ces infos indispensables se trouvent, et qui font donc partie de l'énoncé, pas du texte mais l'énoncé c'est le texte et la figure
à défaut de joindre la figure on la décrit explicitement (très dur quand on n'a pas déja résolu l'exo et donc qu'on "oublie" des détails qui s'avèrent indispensables)

oups c'est moi qui ai raté l'info esentielle "passant par A et D"

RE
Par contre si M est sur OC et N sur OB  avec ON=xV2 on a ON/OB = MN/BC =>
MN = 8xV2/(8V2) = x
et l'aire du trapèze rectangle = (AD+MN)*AN/2 =(8+x)*AN/2
et d'après le f(x) de l'énoncé  il faudrait croire que AN =V((8-x)²+x²) que je ne vois pas ( à chercher)
le mieux est de joindre  la figure avec l'énoncé
peut-être la suivante

A+

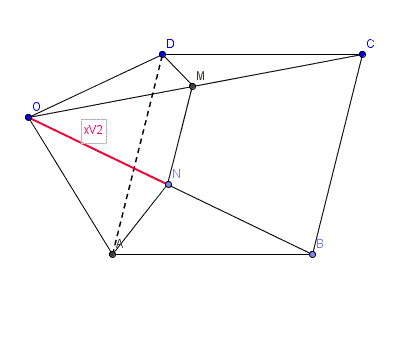
Pour obtenir le AM souhaité, il "suffit" de considérer Al-Kashi dans OAM :
(avec les noms de l'énoncé, c'est M pas N)

AM² = OA² + OM² - 2.OA.OM.cos(45°) = 8² + 2x² - 16x = (8² - 16x + x²) + x² etc

maintenant, sans Al-Kashi c'est plus dur :
application de divers Pythagore + des astuces sur les aires ... bof.

Sans Al Kashi c'est plus facile ...

Au fait, pour le coup de M sur OB ou OC etc

il sufit de bien lire l'énoncé et pas de "croire l'avoir lu"
on est tous tombé dans le panneau.

la pyramide est bien définie comme OACBD donc de base le carré ACBD et pas ABCD :

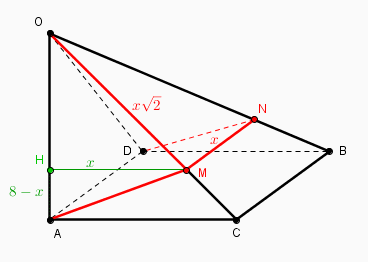
tout est beaucoup plus clair alors !

RE
En effet il faut bien lire
En effet la pyramide est OACB donc de base le carré ACBD
Tout est clair ainsi
et f(x) =  f(x)=1/2(x+8)((8-x)²+x²)
dont la dérivée = 0 pour x=2 qui donne un minimum
ouf
A+