Inscription / Connexion Nouveau Sujet
Fonction de reference
bonjour jai actuellement un exercice a faire sauf que je suis bloquée:
soit f la fonction definit sur R\{3} par f(x)= (x^2-5x+5)/(x-3)
On souhaite etudier la position de la courbe C representant f par rapport a la droite d d'equation: y=x-2.
a) Etudier le signe de f(x)-(x-2) apres lavoir ecrit sous forme fractionnaire
b) En deduire les position relatives de la courbe C et de la droite d
c) DEcrire la foncon dont evolue la valeur de f(x)-(x-2) lorsque x devient grand (tester quelques valeurs de x comme 10^2, 10^3, 10^6...)
Interpreter geometriquement ce phenomene
pour la a:
j'ai (-1)/(x-3) Mais apres je bloque sur letude de signe
Sinon ca veut dire qu'on fait:
-1 est negatif
Si x>3 alors positif
Donc neagtif/positif donne positif
Ou
-1 est negatif
Si x<3 alors negatif
Donc negatif/negatif donne positif
Sinon ca veut dire qu'on fait:
-1 est negatif
Si x>3 alors positif
Donc negatif/positif donne positif tu corriges
Ou
-1 est negatif
Si x<3 alors negatif
Donc negatif/negatif donne positif OK
si x<3 alors f(x)-(x-2)>0 OK
tu en déduis que
la courbe représentant la fonction f est ............ de la droite d'équation y=x-2
-1 est negatif
Si x>3 alors positif
Donc negatif/positif donne negatif
alors f(x)-(x-2)<0
Ou
-1 est negatif
Si x<3 alors negatif
Donc negatif/negatif donne positif
alors f(x)-(x-2)>0
la courbe représentant la fonction f est ............ de la droite d'équation y=x-2
La je vois pas
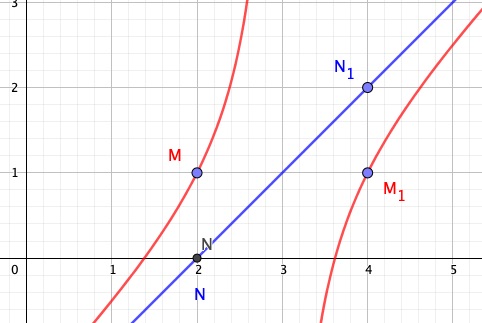
M(x;f(x)) et N(x,(x-2))
si x>3 alors
f(x)-f(x-2)<0==> f(x)<........
donc le point M est ........... du point N
-1 est negatif
Si x>3 alors positif
Donc negatif/positif donne negatif
alors f(x)-(x-2)<0 equivaut a dire f(x)<(x-2)
Ou
-1 est negatif
Si x<3 alors negatif
Donc negatif/negatif donne positif
alors f(x)-(x-2)>0 equivaut a dire f(x) > (x-2)
donc pour x appartenant a ]-infinit;3[ la courbe C passe au dessous de la droite d
et pour x appartenant a ]3; +infinit[ la courbe C passe au dessus de ladroite d
Si x>3 alors positif alors f(x)<(x-2) OK
et tu conclus
la courbe C passe au dessus de la droite d ???
Si x<3 alors f(x) > (x-2) OK
et tu conclus
donc pour x appartenant a ]-infinit;3[ la courbe C passe au dessous de la droite d
???
Si x>3 alors positif alors f(x)<(x-2)
et tu conclus
la courbe C passe au dessous de la droite d
Si x<3 alors f(x) > (x-2)
et tu conclus
donc pour x appartenant a ]-infinit;3[ la courbe C passe au dessus de la droite d
t
oki apres pour la c :
la valeur de f(x)-(x-2) diminiue lorsque x devient plus grand.
Jai fait un tableau de valeurs avec x= 10^2, 10^6, 10^9
Jai trouve -102,07, -1000002 ET -1000000002
Apres je ne vois pas comment interpreter geometriquement ce phenomene
pour la question c
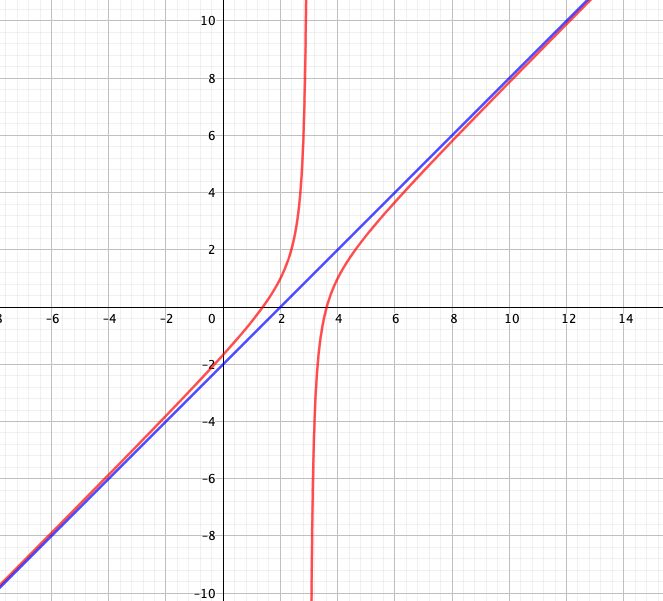
regarde l'écart entre la courbe rouge représentant la fonction f et la droite bleue d'équation y=x-2
que constates-tu ?
Non , tu n 'as pas compris la courbe rouge est de plus en plus proche de la droite bleue
f(x)-(x-2) tend vers zéro quand x tend vers l'infini .
la droite bleue n'est pas un axe de symétrie pour la courbe rouge