Inscription / Connexion Nouveau Sujet
Fonction dérivée et position relative
Bonjour
Je rencontre quelques soucis dans un exercice de maths concernant les fonctions dérivées. (ce sont des révisions de 1ere)
(J'ai joint (Cf) à ce sujet pour que vous puissiez visualiser la fonction et sa tangente).
La consigne de l'exercice : "La courbe (Cf) d'une fonction f, définie sur l'intervalle I = [0;6], et sa tangente au point d'abscisse 6 sont données ci-dessous.
Par lecture graphique
1. Donner le tableau de variation complet de f sur I (signe de f'(x), variations de f).
2. Donner une équation de la tangente à la courbe (Cf) au point d'abscisse 6.
3. Résoudre dans I l'inéquation : f(x)  1"
1"
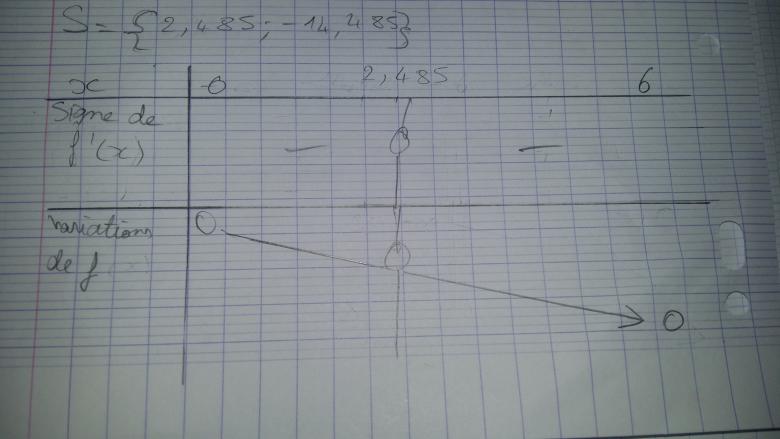
J'ai fais la 1ere question et j'ai obtenu que f est décroissante dans l'intervalle I [0;6] après avoir étudié le signe de f'(x) que j'ai trouvé négatif.
A la 2e question j'ai trouvé que l'équation de la tangente est y= - 0.5x + 3.
Et enfin, je bloque sur la 3e question car la fonction f n'est pas donné dans l'énoncé, uniquement sa représentation graphique, je ne sais pas comment m'y prendre pour calculer l'inéquation sans la fonction et ainsi uniquement avec la représentation graphique.
J'espère que vous pourrez m'aider.

Vu que tu n'as pas l'expression de f(x) , tu résouds graphiquement l'inéquation : il suffit de trouver le ou les points dont les images sont inférieurs ou égales a 1.
Concernant la variation de f je me suis contentée du signe de la dérivée de f que j'ai déduis négatif, et j'ai tracé la variation de f (décroissante) en-dessous.
D'accord, alors si j'ai bien compris tous les points compris dans l'intervalle [0;6] sont tous solution de l'inéquation ? :/
Oui et bien ils sont tous compris étant donné que la fonction f est la petite courbe en dessous, la droite étant la tangente non ?
D'accord, alors tous les points de l'intervalle sont solution, mais du coup je ne justifie pas ? Je dis seulement d'après le graphique .. et je réponds ?
Je voulais également votre avis pour la suite de cette exercice. En faite la suite contient ces même questions sauf que cette fois on nous donne l'expression de f qui est f(x) = (6x-x²)/(x+6). Le soucis c'est qu'en répondant par exemple à la question "Déterminer une équation de la tangent (T) à la courbe (Cf) au point d'abscisse 6", je n'obtiens pas la même équation qu'avec le graphique : avec l'expression de f j'obtiens y = -2/3x + 4 alors qu'en me servant uniquement du graphique j'ai obtenu y = - 1/2x + 3 :/
Concernant la dérivée j'ai trouvé f'(x) = (-x² - 12x + 12)/(x+6)².
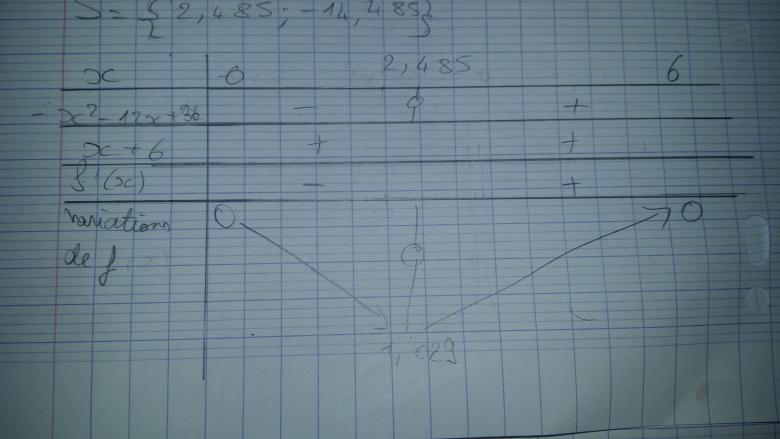
Ensuite j'ai fais delta du numérateur qui m'a donné 2 solutions : 0,928 et -12,928 (dans la question il est dit de "Donner une valeur décimale approchée du maximum, arrondie à 10-3" puis je me suis occupée du dénominateur, afin d'étudier les variations de f. J'obtiens un tableau de variations qui diffère totalement de celui que j'avais obtenu avec uniquement la représentation graphique de la courbe et sa tangente (j'ai joint le tableau de variations que j'obtiens avec l'expression de f) et quant au tableau que j'obtiens avec uniquement la représentation graphique il est composé d'une seule variation de f qui est décroissante car le coefficient directeur de la tangent est négatif.
Normalement je devrais obtenir les mêmes réponses non ? :/
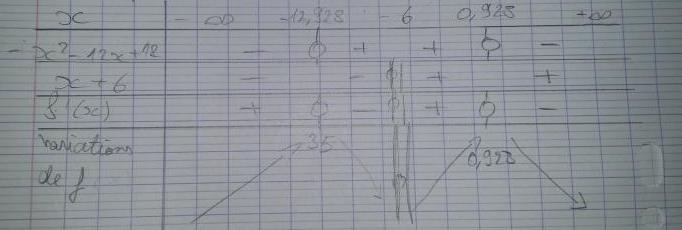
J'ai trouvé l'erreur dans les calculs merci ^^ du coup f'(x) = (-x² - 12x + 36)/(x+6)². En faisant le delta du numérateur j'obtiens cette fois encore 2 solutions : 2.485 et -14.485. Cependant étant donné que l'intervalle est [0;6] je ne mets que 2.485 dans le tableau ? Et pour le dénominateur je trouve une valeur interdite pour la fonction en -6, étant donné que -6 n'est pas dans l'intervalle [0;6] je ne le mets pas non plus ?
que vient faire ce x+6 dans ton tableau
quel est le dénominateur de ta fraction (dérivée) ?
laisse 6( 2 - 1) comme valeur de x et non la valeur approchée
2 - 1) comme valeur de x et non la valeur approchée
Il a changé car je m'étais trompée dans le calcul de f'(x) (j'avais calculé delta avec -x² - 12x + 12 et après avoir corrigé mon erreur j'ai recalculé delta avec -x² +12x + 36) c'est pour cela que les solutions que j'ai trouvé on changé.
ça va pas...ça n'avance pas
reprends la dérivée
écris les valeurs qui l'annulent ou la valeur
étudie correctement le signe de la dérivée
enfin, fais un tableau correct
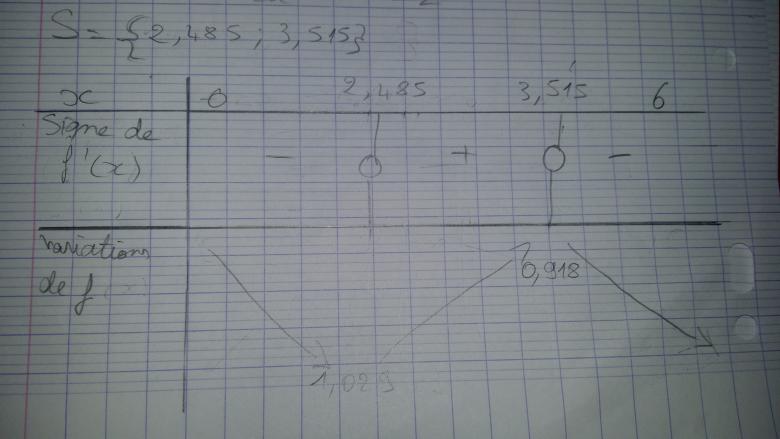
Ah oui ! Je m'étais trompée dans le calcul d'une des solutions, donc les solutions de delta sont : 14,485 et -14,485 (en effet c'est plus logique ^^') Donc étant donné qu'aucune n'est comprise dans l'intervalle [0;6] le tableau est comme ça :
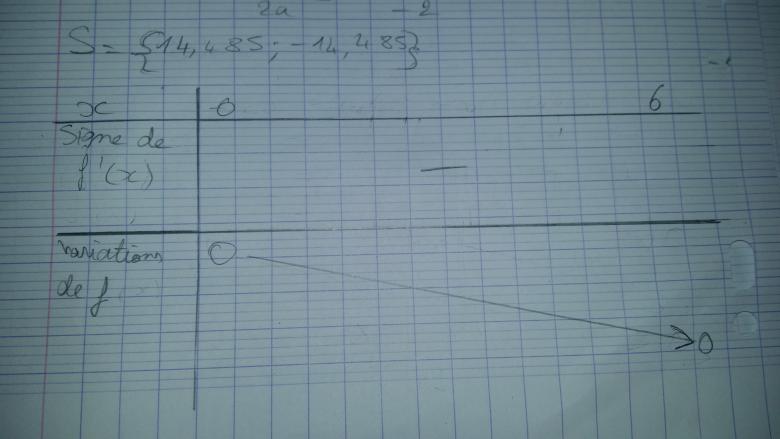
je crois que je vais renoncer, tu n'en fais qu'à ta tête...cela fait je ne sais combien de fois que tu balances des tableaux, tous faux, et tu refuses de donner les intermédiaires, qu'on voie tes erreurs
cf 12h32
Voilà la démarche depuis le début
** image supprimée **![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
croissant de un peu plus de 1 à un peu plus de 0.9, tu as vraiment besoin de nous pour voir que c'est nawak ?
J'ai trouvé l'erreur dans les calculs merci ^^ du coup f'(x) = (-x² - 12x + 36)/(x+6)².
-x²-12x + 36 = - (x² + 12x) + 36 = -(x+6)²+2*36 = 2*6²-(x+6)² = (6
 (2) - (x+6))(6
(2) - (x+6))(6 (2) + (x+6)) = (6
(2) + (x+6)) = (6 (2) - 6 - x)(6
(2) - 6 - x)(6 (2) + 6 + x)
(2) + 6 + x)la deuxième parenthèse est positive puisque x est positif
le signe de la dérivée ne dépend donc que de la première parenthèse, qui change de signe pour x = 6
 (2) - 6 = 6(
(2) - 6 = 6( (2) - 1)
(2) - 1)tu ne devrais rien avoir d'autre que 0 ; 6(
 (2) - 1) et 6, dans la première ligne de ton tableau (et certainement pas de nombre décimal, à part 0 et 6)
(2) - 1) et 6, dans la première ligne de ton tableau (et certainement pas de nombre décimal, à part 0 et 6)Je ne comprends pas à quoi correspondent vos parenthèses contenant des racines carrées. Car moi je fais delta du numérateur de la dérivée et j'obtiens 2 solutions (12-2 2)/(-2) et (12+2
2)/(-2) et (12+2 2)/(-2) et également le -6 qui est la valeur interdite de la dérivée.
2)/(-2) et également le -6 qui est la valeur interdite de la dérivée.