Inscription / Connexion Nouveau Sujet
Fonction dérivée et position relative
Bonjour
Je rencontre un problème dans un exercice, c'est très simple, je suis consciente qu'il est question de tangente et de sa limite mais je ne sais pas par où ni comment commencer pour avancer vers la solution. J'ai commencé à tracer des flèches concernant les mesures qu'il nous est donné dans l'énoncé.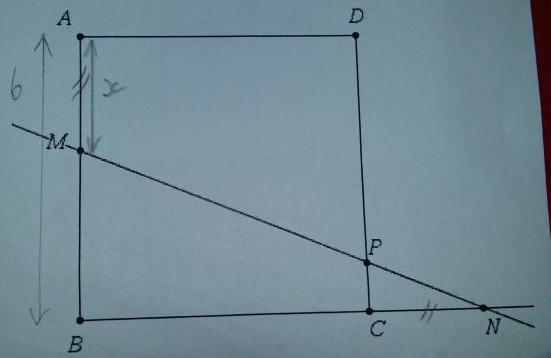 
Si vous pouviez me guider à travers quelques pistes je vous en serai fort reconnaissante 
Voici l'énoncé : "ABCD est un carré de côté 6. M est un point du segment [AB].
Sur la demi-droite [BC), on place le point N tel que CN = AM.
La droite (MN) coupe (DC) en P.
On pose AM = x avec 0
x6.
Déterminer la valeur de x pour laquelle la longueur PC est maximale".
J'ai essayé d'utiliser Thalès mais on a pas assez de renseignements, alors je bloque. Puis je me suis dis qu'il y avait peut-être moyen de connaître PC en utilisant Pythagore vu qu'il y a un triangle rectangle, sauf que je bloque pour le calcul de ((-x²+6x)/6)² 
image recadrée sur la figure (ah ? on me dit dans l'oreillette qu'il n'y en a pas ?)
Annuler
connectez vous