Bonjour, je suis nouveau sur le site ! Merci de votre aide en avance
Alors voilà, je n'arrive pas à savoir que faire dans le devoir maison, je le trouve compliqué.

Voici le sujet qui est un peu long :

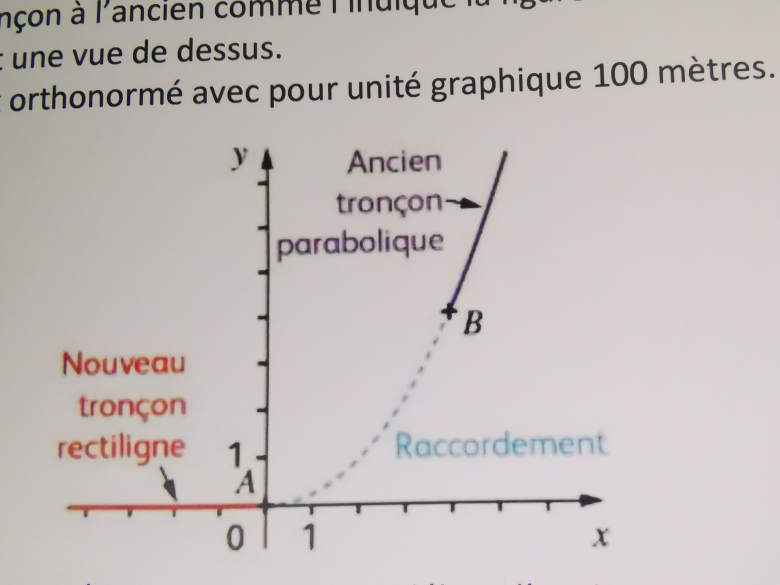
Après rénovation d'un tronçon autoroutier, on souhaiterait raccorder ce nouveau tronçon à l'ancien comme l'indique la figure, qui est un repère orthonormé avec pour unité graphique 100 mètres (pièce-jointe).

Un relevé topographique permet de modéliser l'ancien tronçon par la parabole d'équation y= 0.3x² - 0.2x, le point de jonction B ayant pour coordonnées (4 ; 4).

Le nouveau tronçon est une demi-droite horizontale d'origine A (0 ; 0). Pour des raisons de confort de conduite et de sécurité, le raccordement doit être tangent à chacun des tronçons.

On modélise la courbe raccordant les deux tronçons par la courbe représentative d'une fonction définie sur l'intervalle [0 ; 4] par : f(x) = ax^3 + bx² +cx + d
a b c et d étant quatre constantes à déterminer, a étant non nul.

1. Justifier que f(0) = f'(0) = 0 puis, en déduire les valeurs de c et d puis une nouvelle écriture de f(x)

2. Déterminer les valeurs de f(4) et f'(4). En déduire un système vérifié par les constantes a et b. En déduire l'expression de f (x).