Inscription / Connexion Nouveau Sujet
Fonction dérivées
 Devoirs33
Devoirs33Bonsoir à tous,
J'aimerai de l'aide pour cette exercice s'il vous plaît.
Exercice 1 :
a)Soit une fonction f représentée par la courbe C. La tangente T à cette courbe au point d'abscisse 4 a pour équation y = -5 + 10x. En déduire la valeur de f'(4)
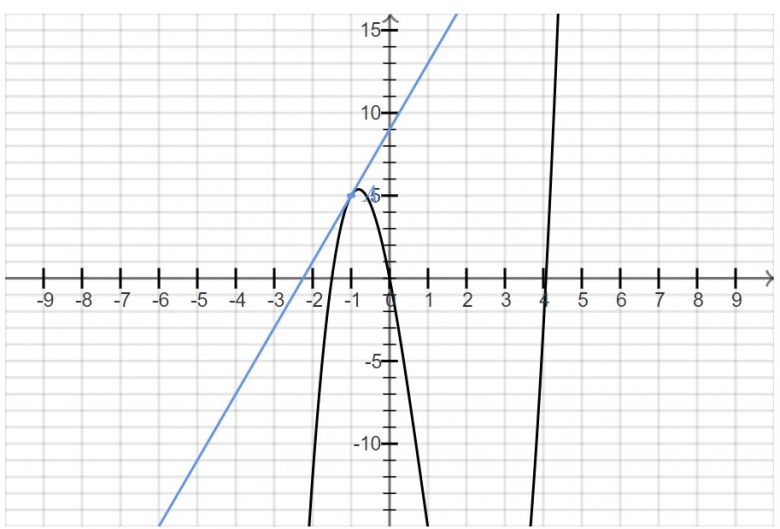
b)Soit f une fonction représentée par la courbe C en pièce jointe.
Déterminer graphiquement l'équation de la tangente à C au point d'abscisse -1.
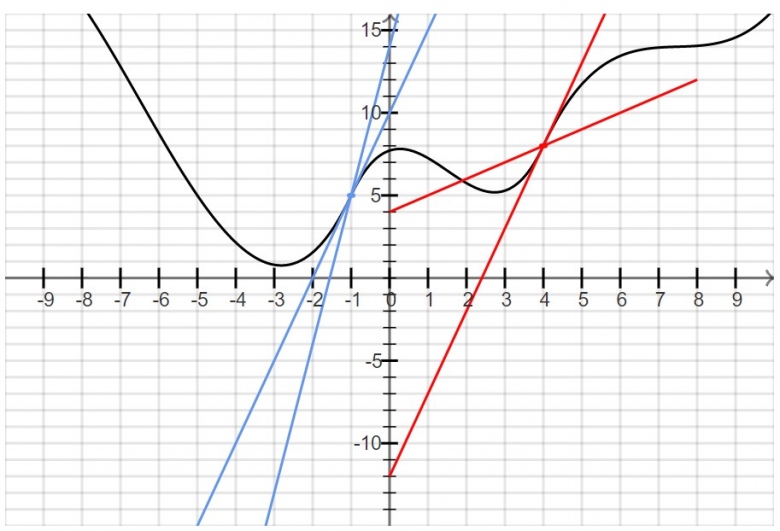
c)Sur la figure en pièce jointe, Cf est la courbe représentative d'une fonction f dérivable sur R. Deux des 4 droites sont tangentes à la courbe C.
Complète le tableau à l'aide du graphique :
f(-1) | ...
f'(-1)| ...
f(4) | ...
f'(4) | ...
d) Quelle est la dérivée de la fonction f ?
On admettra qu'elle est dérivable sur chaque intervalle contenu dans son domaine de définition D = R \ {-3/5}
f :x -->
Merci beaucoup et bonne soirée.
Pour l'instant j'ai essayé de faire la 1 et j'ai trouvé un raisonnement que je partagerai dans quelques minutes.
Non, c'est faux
Par définition, que vaut le coefficient directeur de la tangente au point d'abscisse a ?
Ne crois tu pas devoirs 33 qu'il serait bon de terminer chque exercice avant de passer au suivant?
Bonsoir à tous ...
"Le coefficient directeur est 5 car la tangente de la courbe frôle à 5"
Il y a une règle : tu ne dois jamais employer des mots que tu ne comprends pas. Strictement jamais. Et ici, il y a au moins 2 ou 3 mots ou expressions que tu ne comprends pas.
Tu parles de 'coefficient directeur', ça veut dire quoi, cette expression ?
On est sur la question a)
Fais comme si l'exercice s'arrêtait là. Ne regarde pas les dessins en-dessous.
Bonjour,
Le coefficient directeur est le nombre qui permet de décrire le sens de l'inclinaison. Dans une équation du second degré, elle permet de savoir si les "branches " de la parabole sont vers le haut ou vers le bas.
On peut le calculer avec la formule : xB - xA / yB - yA
Oui, mais ça, ça marche uniquement quand on connaît deux points de la droite
Ici ce n'est pas le cas. Tout ce qu'on sait de la droite c'est qu'elle est tangente à la courbe d'une fonction dérivable. Et là il faut aller voir le cours si tu n'as pas la réponse
Juste une remarque
le coefficient directeur est
Ce qui est écrit est l'inverse du coefficient directeur
D'accord merci pour la formule.hekla
Etant donné qu'on a y = -5 + 10x.
fonction affine du type y = ax + b
le coefficient directeur est 10 ? ( puisqu'il est précédé de x )
Merci
En l'absence de Zormuche
Équation de la tangente au point d'abscisse 4 le coefficient directeur de cette tangente est 10. C'est aussi le nombre dérivé de
en 4 donc on a bien
b) que proposez-vous ?
y = ax + b (l'ordonné à l'origine c'est lorsqu'elle coupe l'axe )
y = ax + 9
le coefficient directeur doit être calculer avec la formule ou graphiquement ?
je vais utiliser la formule : yB - yA / xB - xA
Je choisis un autre point B au hasard car j'ai déjà A :
A ( -1; 5) ; B ( -3; -5)
(-5 - 5) / (-3 - (-1)) = 5 donc si je ne me suis pas trompé le coefficient directeur est 5 donc l'équation de la tangente est
y = 5x + 9 ( sauf erreur de ma part, encore une fois)
Ce n'est pas particulièrement le mien
l'équation de la tangente est en A :
Il s'agit bien du premier graphique, le point que vous avez choisi provenait du second graphique
Pour une prochaine fois, afin que les graphiques suivent bien la question
vous écrivez votre question, insérez une image vous cliquez dessus, vous aurez alors img1 vous posez la deuxième question et même procédé
D'accord merci.
Pour la c) deux des quatre droites sont tangentes à la courbe
Je pense à la droite rouge qui touche -12 à l'axe des ordonnées et à la droite bleu qui touche -2 à l'axe des abscisses ( à confirmer)
f(-1) = 5 ?
Je pensais en regardant le graphique vous pouviez constater que les deux droites étaient bien parallèles


