Inscription / Connexion Nouveau Sujet
fonction exponentielle
Bonjour
Problème 11
Le plan est muni d un repère orthonormé (o,i,j) ,unité graphique ,2 cm.
On considéré les fonctions f et g définies sur R par :
f(x)=e^x-x^2 et g(x)=e^-x-x^2
C1 et c2 designent les courbes représentatives respectives de f et g dans le repéré (o,i,j)
Partie A
1/ calculer les limites de f aux bornes de son ensemble de définition
2/ justifier que tout x de R ,f'(x)=e^x-2x et f"(x)=e^x-2
3a étudier le sens de variation de f
b/ dresser le tableau de variation de f
5a/ tracer, la range (T) a c1 au point J
b/ trouver une équation de (T)
6/a/ justifier que f a un unique zéro a;
b/ justifier que : -0,71<a<-0,70
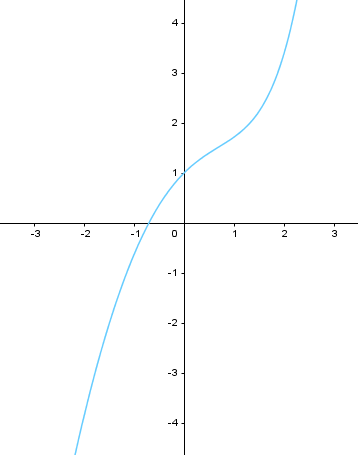
7a/ justifier que la courbe r: y=-x^2 est une asymptote a (c1) en + infini,
b/ étudier la position relative de C1 et r
8 /a/ calculer en -infini et + infini
Lim f(x)/x
b/ interpréter graphiquement les résultats obtenus.
9/ construire (r) et c1 dans un même repéré.
Partie B
1/ vérifier que, pour tout nombre réel x ,g(-x)=f(x)
2a/ calculer g(-a)
b/ justifier que -a est l unique zéro de g
3a/ donner un programme de construction de C2 a partir de c1 a la règle et au compas
b/ construire C2 a partir de c1
Réponse
Question 1
En + infini
Lim f(x)=lim e^x(1-x^2/e^x)
Lim e^x=+ infini et lim 1-x^2/e^x)=0
Lim f(x)=+ infini
En - infini
Lim f(x)=+ infini
Question 2
f'(x)=e^x-2e^x-2x
f''(x)=e^x-2
Question 3a
J ai besoin d aider
Bonjour
Pourquoi vous demande-t-on la dérivée de f' ? Pour avoir le sens de variation de cette fonction et pouvoir déterminer le signe de et par la suite celui de
Bonjour
Vraiment dire , moi je n ai aucune idée. C est un exercice que le professeur nous a donné a faire a la maison
Est ce que vous pouvez m aider s il vous plaît
Je vous ai donné la réponse
étudiez la fonction
Pour cela étudiez le signe de c'est-à-dire
de la dérivée de
donc sens de variation de
Maintenant vous avez le signe de
et vous pourrez déduire le sens de variation de
On étudie le signe de f'(x) c'est tout,
Quand est-ce que :
Or tu te retrouves un peu bloqué ici donc tu passes à f''(x) :
Tu continues puis dresse le tableau de signe de f'' t'en déduit les variations de f' et regarde de plus près les valeurs car ce que tu veux c'est avoir le sens de variation de . Si f'(x) > 0 alors f croissante et inversement.
À partir de là tu peux le faire ! 
bonsoir,
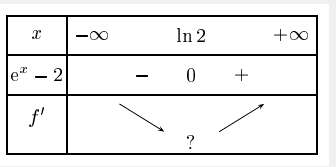
tu te trompes pour le signe de ]a dérivée seconde,elle s'annule en changeant de signe donc f' n'est pas croissante su r 
Il faut que tu cherches les intervalles ou la dérivée seconde est positive et negative :
Il faut résoudre l'inéquation :
Tu connais ln(x) ? Tu peux t'en servir ici pour trouver la valeur à partir de la quelle e^x est supérieur â 2
Ln(x) permet d'enlever le exponentiel :
Si tu veux la traduire en phrase l'inégalité, ça revient à :
La dérivée seconde est > 0 quand x > ln(2)
Donc quand c'est avant ln(2) c'est inférieur
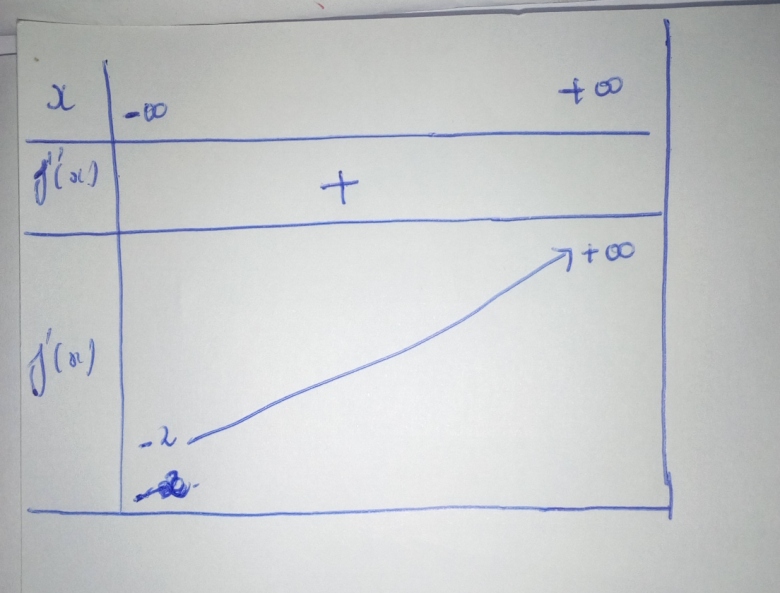
Sens de variation de
Que vaut Que peut-on en déduire quant au signe de
?
Enfin au sens de variation de
Justement pour savoir que est croissante il faut bien que
soit positive donc on a bien besoin du signe de
que vous le fassiez par un tableau ou en ligne, peu me chaut
Question 4
Pour tout nombre réel x, f'(x)>0, donc f est strictement croissant .
Dresser le tableau de variation de f
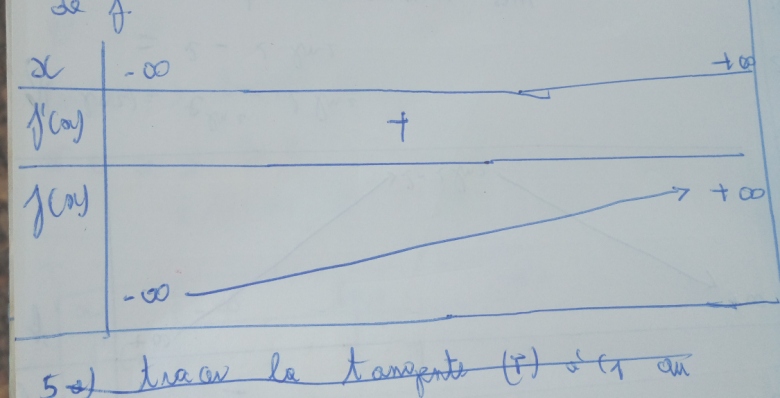
Il semblerait qu'il faille lire à la question 3 et
alors à la question 4.
Que proposez-vous pour 5 a) ?