Inscription / Connexion Nouveau Sujet
Fonction exponentielle bac C (années 70) pour correction 
Bonjour, j'ai gardé mes sujets de bac C (années 70) et je pense pouvoir faire maintenant l'exercice sur lequel j'ai bloqué à l'époque (dans la marge du sujet, j'ai écrit 2/4…je n'ai pas gardé mon brouillon)
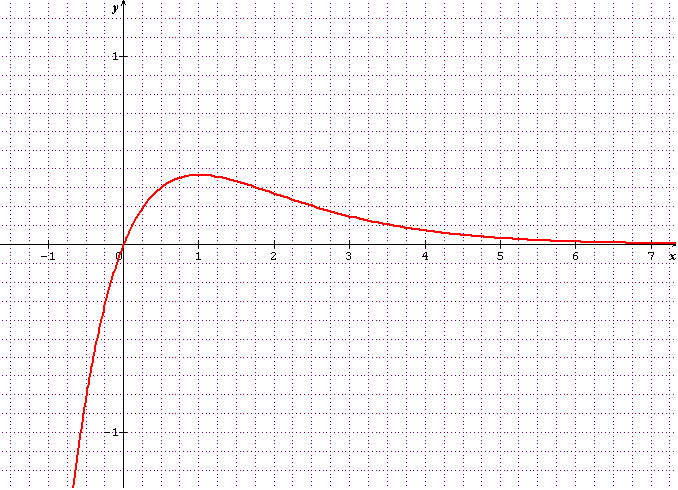
1) Etudier les variations et tracer la courbe représentative (C) de la fonction numérique définie sur IR par f(x) = x*e^(-x).
En déduire que pour a > 0 et distinct d'une valeur que l'on précisera, il existe un seul réel b, différent de a, tel que a*e^b = b*e^a.
2) Calculer l'aire du domaine délimité par (C), son asymptote et les droites d'équation x=0 et x=t, où t désigne un réel strictement positif. Cette aire admet-elle une limite lorsque t tend vers +00 ?
Question 1
Je cherche les limites en +00 et -00
La limite quand x tend vers -00 de f(x) = x*e^(-x) est -00 car on a un produit de -00 par +00
La limite quand x tend vers +00 est égale à la limite de -x*e^x quand x tend vers -00 c'est à dire 0
On remarque que la courbe passe par l'origine car f(0) = 0
Dérivée : je trouve f ‘(x) = (1-x)e^(-x) qui s'annule pour x=1
Donc ma fonction f est croissante jusqu'à x=1 et décroissante ensuite. Elle admet un maximum pour x=1 f(1) = 1/e
Je peux donc tracer la courbe (C)
Ensuite je dois en déduire que pour a > 0 et distinct d'une valeur que l'on précisera, il existe un seul réel b, différent de a, tel que a*e^b = b*e^a. Je crois me souvenir que j'ai bloqué là dessus.
a*e^b = b*e^a entraîne a*e^(-a) = b*e^(-b) qui ressemble à f(x)
Si on prend a compris entre 0 et 1, on aura une valeur b comprise entre 1 et +00 qui aura même image par la fonction f. En effet, la fonction f est continue et uniformément croissante entre 0 et 1 et continue et uniformément décroissante entre 1 et +00.
J'ai pris un exemple qui le montre sur la courbe : pour a
0.25 on a une valeur b 2.5 qui a même image par la fonction f.
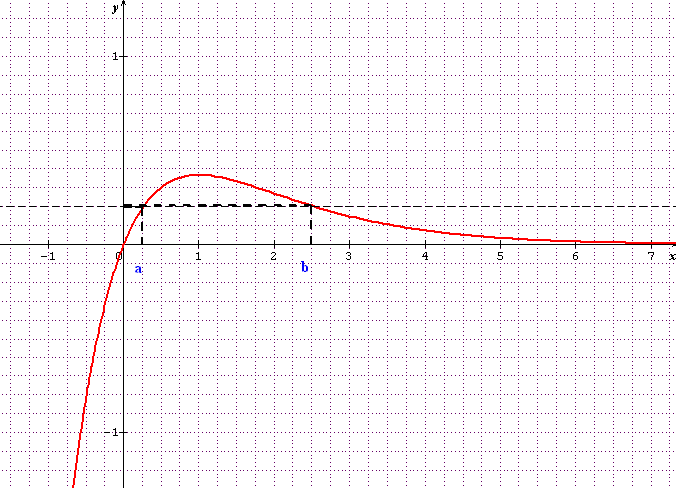
La seule valeur pour laquelle ce n'est pas possible est a=1 qui correspond au maximum de la fonction f.
2) Calculer l'aire du domaine délimité par (C), son asymptote et les droites d'équation x=0 et x=t, où t désigne un réel strictement positif. Cette aire admet-elle une limite lorsque t tend vers +00 ?
Ici, je bloque pour trouver une primitive de f(x) = x*e^(-x). En tâtonnant, sachant qu'une primitive de xe^x est (x-1)e^x +k je trouve une primitive de f(x) : F(x) = -(x+1)e^(-x)
Donc si un « pro » pouvait m'expliquer comment le trouver proprement, ce serait gentil.
Ensuite je calcule l'aire du domaine délimité par (C), son asymptote et les droites d'équation x=0 et x=t
(j'ai calculé F(0) et j'ai trouvé -1)
Quand t tend vers +00 la limite de -(t+1)e^(-t) sera celle de xe^x quand x tend vers -00 c'est à dire 0
Donc quand t tend vers +00 l'aire du domaine délimité par (C), son asymptote et les droites d'équation x=0 et x=t sera 1
Voilà, graphiquement mon résultat est cohérent. J'aimerais savoir si c'est juste, et connaître la bonne manière de trouver une primitive de f(x) = x*e^(-x).
Merci
Bonjour,
pour la primitive de xe-x il te suffit de faire une integration par partie
Pose u=x et v'=e-x
donc u'=1 et v=-e-x
alors F= uv - primitive(uv')
F= -xe-x-primitive(-e-x)
F= -xe-x-e-x+ K
F=-(1+x)e-x+K
Merci les jeunes
Je vais donc revoir le cours sur l'intégration par partie. Je ne pense pas avoir bloqué là-dessus à l'époque, mais sur la question :
En déduire que pour a > 0 et distinct d'une valeur que l'on précisera, il existe un seul réel b, différent de a, tel que a*e^b = b*e^a.
Je la trouve bien tordue. Ma démo actuelle vous semble correcte ?
Si déjà elle va dans la bonne direction, je suis contente. Je me vois encore sécher là-dessus dans le stress de l'examen 
Rapidement moi j'aurais fait comme ça :
On a f qui est continue, strictement croissante sur [0;1] avec f(0)=0 et f(1)=1/e donc f réalise une bijection de [0;1] sur [0;1/e]
De même sur l'intervalle [1;+oo[,f est continue strictement décroissante à valeur dans [1/e;0].
Donc pour tout réel c dans [0;1/e] il existe un unique antécédent par f dans [0;1] (respectivement dans [1;+oo[) donc f(a)=f(b) entraine que a est dans [0;1] et b dans [1;+oo[.
C'est pas super rigoureux non plus mais j'ai pas trop le temps là , enfin c'est l'idée quoi
Pour ma part je t'en prie
La formule des vrais "pros"
Je viens de revoir l'intégration par parties dans un mémobac. Rien de compliqué, finalement.
Je posterai l'autre exo quand j'aurai revu les complexes. Pour celui-là, j'avais marqué 3/4 dans la marge 
Je pense que le programme n'a pas beaucoup changé... il semble que les jeunes d'aujourd'hui n'ont pas de mal à faire les sujets d'autrefois
Je te mets les liens 
Je pense que le programme n'a pas beaucoup changé... il semble que les jeunes d'aujourd'hui n'ont pas de mal à faire les sujets d'autrefois
J-P si tu nous lis
J'essayerais ça dans la semaine, merci borneo !
Bonjour
Je recherche le sujet de maths du bac C année 1970
J'ai vu que Bornéo le possédait mais je n'arrive pas à le joindre
Merci de votre aide
Bonjour
Je recherche le sujet du bac C (en maths) de 1970 , je crois que "Bornéo "le possède mais je n'arrive pas à le joindre
Merci de votre aide
Non mais dites donc... en 1970, j'étais encore au collège 
mon sujet, c'est dans les années 70, mais je ne vous dis pas laquelle...
Demandez à Littleguy, il fait collection de sujets...
Norton, tu as cliqué sur mes liens ? (les petites maisons)
Avec la loupe, on lit très bien les sujets. J'ai aussi la physique-chimie
Annuler
connectez vous