Inscription / Connexion Nouveau Sujet
Fonction exponentielle et dérivée - Exo Type BAC
Bonjour, j'ai un excercice type BAC à faire et il y a certaines questions auxquelles je n'ai absolument aucune idée pour comment y répondre. J'aimerais que ceux qui auront l'amabilité de m'aider prennent un peu de leur temps pour m'expliquer plus en détail avec des notions de cours les réponses aux questions, parce que je suis vraiment perdue dans ce chapitre et même si vous me donniez la réponse cash je ne la comprendrais pas toute seule 
Merci beaucoup !
L'exercice est un extrait d'un type BAC présent sur le site :
1. La courbe ci-dessous illustre l'évolution de la température en degrés Celsius d'une plaque chauffante en fonction du temps écoulé en secondes.
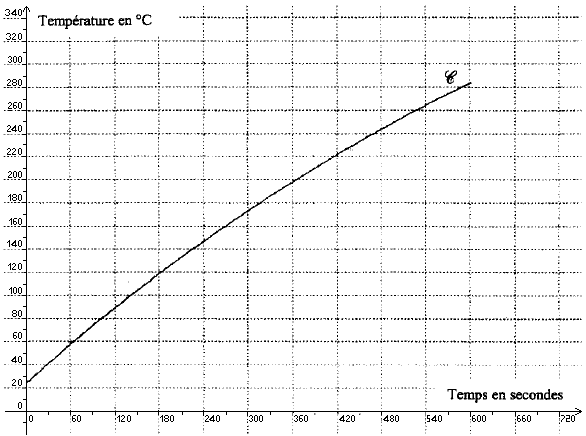
Déterminer graphiquement une valeur approchée de :
a) la température de la plaque au bout de cinq minutes ;
b) l'instant où la température de la plaque atteint 120°C.
2. La fonction représentée à la question 1. est définie sur l'intervalle [0 ; 600] par :
f(t) = 600 - 576e -0.001t
a) On note f' la dérivée de la fonction .
Calculer f' (t) lorsque t appartient à l'intervalle [0 ; 600].
b) Etudier les variations de f sur l'intervalle [0 ; 600].
c) Recopier et compléter le tableau de valeurs ci-dessous en arrondissant au dixième.
| t | 180 | 181 | 182 | 183 | 184 | 185 |
| f (t) |
d) En déduire l'instant, à la seconde près, où la température de la plaque atteint 120°C.
e) Résoudre l'équation f(t) = 120 sur l'intervalle [0 ; 600] et vérifier que la valeur exacte de la solution est 1000 ln(1,2).
----------------------------
J'ai résolu les 2 premières questions. Merci d'avance à ceux qui proposeront leur aide
1a) Au bout de 5mins, la température de la plaque est entre 20 et 25°C soit d'environ 22,5°C graphiquement.
1b) L'instant ou la température de la plaque atteint 120°C est 180 minutes soit exactement 3h.
Bonjour,
comment as-tu fait pour trouver entre 20 et 25° ?
tu dois te positionner sur le x de l'axe des abscisse qui représente un temps écoulé de 5 minutes et lire en ordonnée la température...
22.5 degrés, c'est supportable ! Essaie un peu de mettre ta main sur une plaque chauffante après 5 minutes ! Aie, aie !
Tu devrais tout d'abord regarder l'échelle sur ton graphique avant de conclure quoi que ce soit. La graduation est en secondes ! Donc, au bout de 5 min, il s'est passé 5*60 soit 300 secondes. Et le graphique indique que la température est alors environ 165 degrés. Je te déconseille donc de mettre ta main sur une plaque chauffante mise en marche cinq minutes auparavant !
De même, la plaque atteint 120° au bout de 180 secondes, soit 3 minutes ! Si une plaque chauffante met 180 minutes (soit 3 heures !) pour atteindre la misérable température de 120° de combien de temps la ménagère aura-t-elle besoin pour cuire deux oeufs sur le plat ? Il faut être raisonnable ! Et attentif !
Pour la question 2a, tu devrais savoir la dérivée de ekx : c'est kekx. Donc la dérivée de :
e(-0.001 t) est -0.001 e(-0.001 t)
A présent, calcule la dérivée de f !
Ah oui! Je me disais aussi que quelque chose n'allait pas et que ça prenait beaucoup de temps a chauffer je n'ai pas réalisée que c'était en secondes et non en heures. Désolée haha je suis vraiment à l'ouest
Je dois calculer f'(x) = 600 - 576( -0.001 
e(-0.001 t) ?
En tout cas si c'est ça... Je ne sais pas du tout comment faire.
Je sais juste dérivé des fonctions basiques mais celles la me semblent vraiment compliquées, on peut m'expliquer s'il vous plait ? :S
Donc je developpe 576(-0.001 e-0.001t ce qui donne -576 e-0.001t et comme la dérivée de 600 donne 0 alors :
0 - ( - 0.576 e[sup]-0.001t[/sup donne 0.0576 e[sup]-0.001t[/sup.
Juste ?
Et j'ai résolu le reste mais j'ai besoin d'une correction la aussi parce que je ne suis sure de rien...
Les variations de f : Sachant que 0.0576 est positif et que l'exponentiel l'est toujours, un produit de deux facteurs positifs sera lui même positif. Donc :
oui
la dérivée de -0.001t est -0.001 donc tu auras :
f(t)=600-576e-0.001t ==> f'(t)= -576-0.01-001t donc f'(t)=0.576e-0.001t
ok pour les variations f(t) toujours croissante sur [0;600]
Désolée, j'ai postée trop vite :
| x | -  + |
| f(x) | 0  600 |
( Oui bon... je n'arrive pas a dessiner une longue fleche qui monte
)
c)
| t | 180 | 181 | 182 | 183 | 184 | 185 |
| f(t) | 118.9 | 119.4 | 119.8 | 120.3 | 120.8 | 121.3 |
d) La température atteint 120°C à environ 183 secondes soit 3minutes et 3secondes.
( 119.8 est plus proche de 120 que 120.3 mais comme à 119 on n'a toujours pas atteint 120 je ne l'ai pas mis et j'ai préféré la valeur supérieur, est ce juste ? )
e) Je ne sais pas du tout comment l'expliquer mais sachant que sur la calculette : 1000 ln(1,2) est égal à 182.3215568
lorsque je remplace : 600 - 576e)0.001
182.3215568 cela donne exactement 120 donc c'est vérifié. Mais je ne sais pas comment le démontrer a partir de 600 - 576e0.001t pour la détermination à l'aide du graphique :
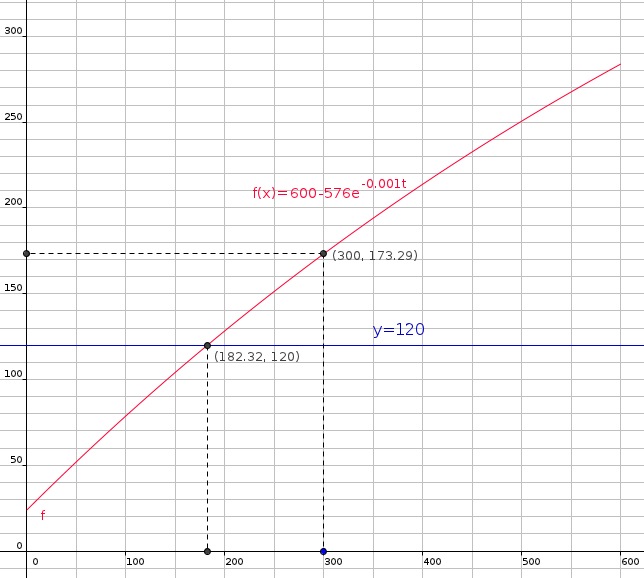
f(t)=120
600-576e-0.001t=120
-576e-0.001t=-480
e-0.001t=480/576
ln(e-0.001t=ln(5/6)
pourrais tu faire la suite ?
Ohh oui je vois, je remplace e-0.001t par 480/576 dans l'expression lne-0.001t=ln(5/6) et le resultat est le meme c'est a dire : -0.1823215558, la valeur exacte.
Merci beaucouppppp !!!
bonjour, pythamède, tu as raison dommage que Heartless se soit désinscrite elle ne pourra même pas en profiter...
Annuler
connectez vous