Inscription / Connexion Nouveau Sujet
Fonction Ln
Bonjour, j'ai de petits problèmes avec mon exercice de maths. Je vous transmets le sujet :
On note f la fonction définie sur l'intervalle ]0;+
) par f(x)=x(2ln(x)+1) et C la courbe représentative dans un repère orthonormé d'unité 2cm.
1)a) Calculer les limites de f aux bornes de son ensemble de définition
b) Etudier les variations de f puis dresser son tableau de variations.
2)Soit un réel a
0. On note Ma le point d'abscisse a de C et Ta la tangente à C en Ma.
a) Déterminer les coordonnées du point d'intersection Ia de Ta avec l'axe des ordonnées.
b) En déduire une méthode simple permettant de construire la tangente Ta
Il y a de questions suivantes mais je pense pouvoir y arriver.
Voici donc mes problèmes :
2)a) On sait que x=0 j'ai trouvé y=a(-2+ln(a)-ln(a2)). Je ne suis pas sur que ceci est juste ni que ma méthode l'ai aussi...
2)b)Je n'ai pas vraiment cerner le but de cette question !
Merci d'avance de votre aide à tous !
Bonjour
vous n'avez pas écrit une équation de droite
une équation de la tangente en est
l'abscisse du point d'intersection de la tangente avec l'axe des ordonnées est bien 0
quelle est la dérivée ?
La dérivée est la suivante : f'(x)=ln(x2)+1
Mais a est strictement supérieur à 0, voilà mon plus gros souci
Tout le sujet que l'on peut avoir besoin est en haut. Le reste des questions que je n'ai pas mises sont sur un calcul d'aire !
Désolé ! Voici le détail :
u(x)=x u'(x)=1
v(x)=ln(x2)-1 v'(x)=2x/x2=2/x
f'(x)=u'v+uv'=ln(x2)-1+(2x/x)=ln(x2)+1
Je viens de remarquer mon erreur c'est un -1 et non pas un +1 désolé !
J'ai préférer marquer ln(x^2) pour une question de simplicité d'après moi bien entendu !
d'accord
remarque ce n'est pas totalement équivalent il faut à chaque fois dire que est strictement positif
Oui en effet je viens de la rajouter sur ma copie ! Pour revenir à la question 2)a) pourriez vous m'éclairer hekla ?
Désolé ! Voici le détail :
u(x)=x u'(x)=1
v(x)=ln(x2)-1 v'(x)=2x/x2=2/x
f'(x)=u'v+uv'=ln(x2)-1+(2x/x)=ln(x2)+1
Je viens de remarquer mon erreur c'est un -1 et non pas un +1 désolé !
J'ai préférer marquer ln(x^2) pour une question de simplicité d'après moi bien entendu !
v(x) = 2 ln x + 1 est de la forme ku + c où k et c sont des constantes donc v'(x) = ku' (cours de première)
v(x) = ln(x^2) + 1 est de la forme ln (u(x)) + c dont la dérivée est u'/u
ce qui nécessite bien plus de calcul
et si tu trouves cela plus simple alors tu ne sais pas calculer parce que tu ne sais pas calculer en pensant (donc en gros tu calcules comme une machine)
or les math c'est penser ...
PS : et ensuite pour le calcul des variations donc du signe de la dérivée c'est à nouveau bien plus long et fastidieux d'étudier le signe de ln (x^2) + 1 que celui de 2ln x + 1 ...
Ah d'accord j'ai compris ! En gros, il y a deux X différents. Un pour f et f' et un autre pour la tangente.
non une équation de droite est une relation entre les coordonnées d'un point pour que ce point appartient à la droite
dans l'équation de la tangente à la courbe représentative de il y a qu'un
si l'on donne une valeur à cet
on peut alors déterminer l'ordonnée du point appartenant à la tangente
il n'y a pas différents
vous trouvez quoi alors ?
il faudrait être plus explicite
si vous dites que l'ordonnée du point d'intersection de la tangente en à la courbe et l'axe des ordonnées alors oui
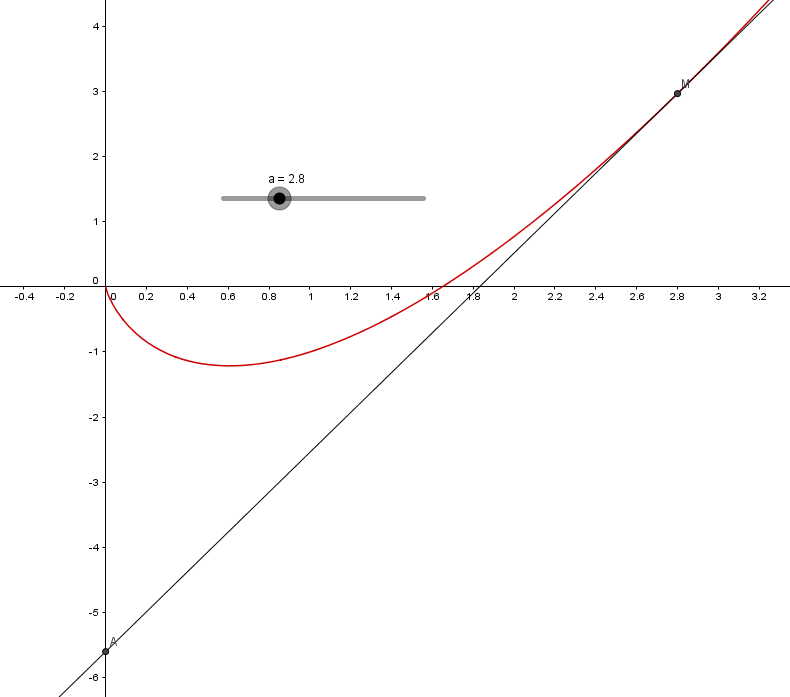
J'ai l'impression de m'être vraiment emmêler les pinceaux pour rien
Pourriez vous reformulez la question 2)b) je ne la comprends pas vraiment ! Merci !
apparemment on vous demande de trouver un procédé pour tracer la tangente en à la courbe
si l'on connait le point de tangence on connait donc
et ayant deux points cela est suffisant pour la tracer
Annuler
connectez vous