Inscription / Connexion Nouveau Sujet
fonction ln avec paramètre m
salut,
voilà l'énoncé :
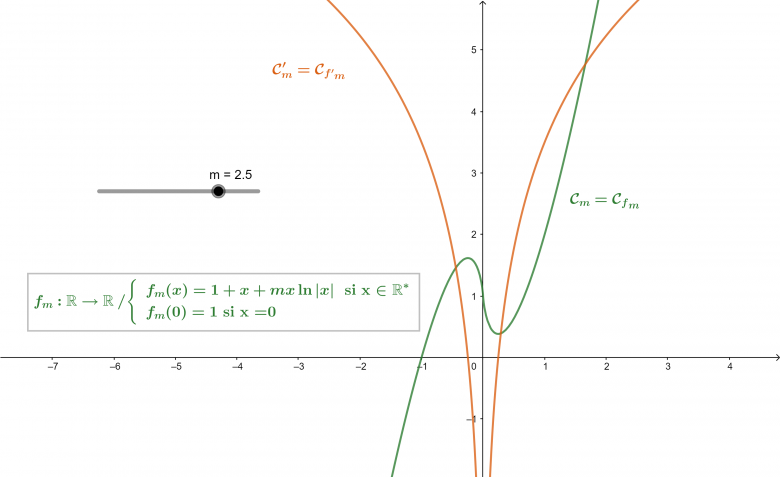
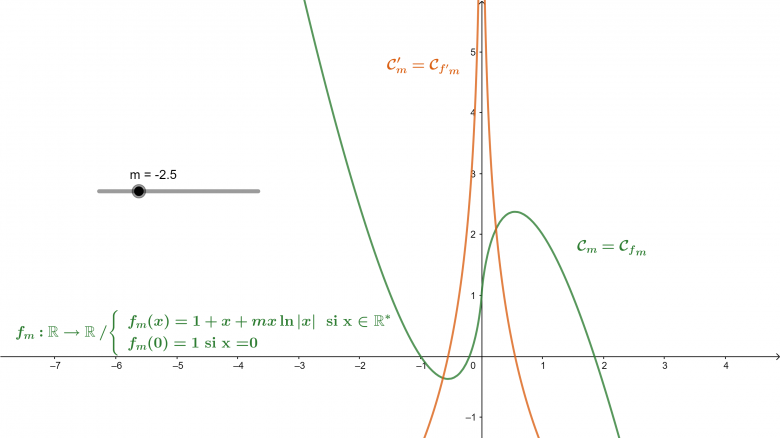
soit fm une fonction définie sur 
par
*fm(x)=1+x+mxln(abs(x)) si x
0
*f(0)=1
1) étudier la continuité de fm en 0
2)étudier la dérivabilité de fmen 0
3) montrer que A(0;1) est un centre de symétrie de la courbe de fm, Cm
4)étudier les branches infinies de la courbe de fm selon les valeurs de m
5)montrer que toutes les courbe Cm passent par trois points fixes qu'on déterminera lorsque m varie sur avec m0
6)étudier les variations de fm
7) montrer que Cm coupe l'axe des abscisses en un point d'abscisse 
avec 
]3;4[
J'ai réussi seulement à faire l qst 1) et 3)
ben par exemple tu calcules l'intersection des courbes C1 et C2, puis tu montres que leurs points d'intersection appartiennent aussi à toutes les autres Cm (avec m non nul)
curlyrhb
extrait de 
la FAQ du forum :Q26 - Pourquoi dois-je écrire mon message dans un français correct ? Pourquoi le langage SMS est-il interdit sur l'Île ?
merci de respecter
Annuler
connectez vous