Bonsoir,

Tu devrais poster ton énoncé en entier et vérifier s' il n' y a pas d' erreur.

En l' état, ta suite est croissante à partir du rang 5.

Bonsoir !
Détermines le signe de et tu sauras la position de et de .

Bonsoir lusak,

Je ne vois pas.

Pourrais-tu en dire plus?

J'ai trouvé une solution assez compliquée... qui utilise en plus le théorème des accroissements finis qui n'est pas du programme de terminales..
Il doit y avoir plus simple..
Mais c'est vrai ce que dit Lake... .. la suite est croissante à partir de n=5

As-tu trouvé le signe demandé ?
Si oui, fais un dessin et, au cas où, reviens nous voir !

J'ai démontré la croissance de la suite..

Bonjour Nofutur2

Il y a des petits problèmes dans l' énoncé; c' est pour ça que je doute:

L' encadrement de n' est valable que si ; ce n' est pas indiqué...

Le "signe demandé" dépend de la place de par rapport à et n' apporte pas grand chose. Il y a ce rang  5 qu' il faut bien faire apparaître à un moment ou à un autre.

Je crois que Lusak a survolé l' exercice dans le style : moui, le signe de , tirez la bobinette et la chevillette cherra

J'ai résolu le problème en me positionnant pour n>=5..
Et çà se justifie dans les calculs..
Je calcule une certaine expression qui doit être positive et ça n'est le cas que pour n>=5...
Mais j'hésite à donner ma solution parce que c'est un peu long..
A moins que ....

Bonjour ,
sans certitude ....

signe de  )


comme les fonctions g_n sont décroissantes  alors

recherche du rang n....à partir duquel  la suite (an) devient croissante    
a₂=1     et  1-(1/2)=1/2<a₂
a₃=0,72..  et 1-(1/3)=2/3 <a₃
a₄=0,8...   et 1-(1/4)=0,75 <a₄
a₅=0,79... et 1-(1/5)=0,8 >a₅

Pourquoi -na_n-1+n>0 ???

C'est justement ce qu'on cherche à démontrer ..non??

je cherche pour quelles valeurs de n  en fonction de a_n le signe de  
g_n+1(a_n )est positif

Moi je suis parti du point d'intersection des courbes représentatives de g_n et g_n+1.
Son abscisse est x_n=1-(1/n).. et mon problème a été de trouver le signe de son ordonnée..
puisque
si x<x_nalors  g_n < g_n+1.
si x>x_nalors  g_n > g_n+1.
Le but a été de démontrer que g_n (x_n)<0 comme les fonctions g_n sont décroissantes...

oui mais tu ne prouves rien.. Tu le supposes..

Je viens de comprendre ... C'est une espèce de récurrence, mais  avec une hérédité un peu rapide..

J'ai démontrer que g_n(x_n)=1+(1-n)*(1-(1/n))^n-ln(1-(1/n))<0 pour n>=5

ou -g_n(x_n)=-1+(n-1)*(1-(1/n))^n+ln(1-(1/n))>0 pour n>=5
en étudiant la croissance de chaque terme..
et c'est (1-(1/n))^n qui m'a donné du mal .. Mais j'ai réussi avec le théorème des accroissements finis..en utilisant le log de la fonction..
Y a peut être plus simple.

J'ai d'abord utilisé le TAF pour la fonction log sur ]n-1,n[
Il existe c ]n-1,n[ tel que 1/c=log(n/(n-1))donc
-1/(n-1)<log(1-(1/n))<-1/n   (1)
Si je pose f(x) = (1-(1/x))^x, on a log(f)=x*log(1-(1/x))
En dérivant log(f)je trouve ln(1-(1/x))+1/(x-1), qui d'après (1) est >0..
comme le log et la fonction varie dans le même sens  f(x) = (1-(1/x))^x est croissante..
ln(1-(1/n)) est évidemment croissante..
Donc pour n>=5 -g_n(1-(1/n))>-g_n(1-(1/5))=1,323-0,223+10,089>0

Donc _n< _n+1<x_n=1-(1/n)... et la suite(_n) est croissante à partir de n=5...

    j'ai aussi  voulu chercher le signe de g_n(1-(1/n))=1+(1-n)*(1-(1/n))^n-ln(1-(1/n),mais j'ai abandonné...bravo pour ta  démo
  
  comme  dit lake

Je viens de m'apercevoir que tu avais "pratiquement" raison..
Je devais être mal réveillé ce matin quand j'ai trouvé cette démo un peu tordu...
Oui tu as raison, une simple récurrence marche.
Elle porte sur le signe de l'ordonnée du point d'intersection de la courbe de g_n et g_n+1,
de coordonnées x_n=1-(1/n)
La propriété P_n à démontrer est "g_n(x_n)<0"
Initialisation:
On calcule g₅(x₅)soit g₅(0,8)=g₆(0,8)... et on trouve g₅(x₅)=g₆(x₅)<0..
Donc P₅ est vraie.
Hérédité :
On suppose que "g_n(x_n)=g_n+1(x_n)<0".
Comme x_n+1=1-1/(n+1)>x_n et que g_n+1est décroissante.. l'ordonnée du point d'intersection des courbes de g_n+1 et g_n+2 est inférieure à g_n+1(x_n),
Donc g_n+1(x_n+1)=g_n+2(x_n+1)<g_n+1(x_n)<0
Donc P_n+1 est vraie.
Conclusion :
Ca marche !! et la suite alpha est croissante à partir de n=5 ..

Effectivement,ça marche!

Tu me croiras si tu veux, j' avais fait ce dessin sur Geogebra hier matin avec les points et d' abcisses ... puis abandonné.
J' ai juste rajouté les noms de courbes pour qu' on y comprenne quelque chose:



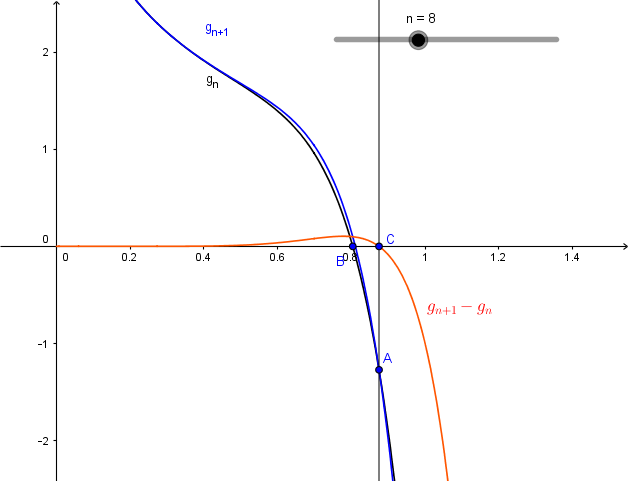
Encore

Mais bon je persiste à croire qu' on peut difficilement demander ça en terminale

Salut Lake !!
Joli problème en effet,.. Ça m'a permis de me replonger dans le théorème des accroissements finis, .. même si finalement la solution était plus simple..
C'est quand même super géogébra !!
A+

Au fait, j'ai pensé à toi en écrivant ..

-1/(n-1)<log(1-(1/n))<-1/n  

C'est toi le champion des encadrements géniaux !!

Faut pas exagérer!!!

En fait, je suis du Maroc et on a déjà fait le théorème des accroissements finis parce que ça fait partie du programme du terminale au Maroc.  Mais comment on peut résoudre ce problème en utilisant TAF?

Alors regarde la solution (20/12  à 16h01)..