Inscription / Connexion Nouveau Sujet
Fonction Logarithme népérien.
Bonjour à tous, j'ai un exercice de math qui me pose vraiment problème, j'aurais besoin de votre aide!
Voici l'énoncé:
Soit f la fonction définie sur l'intervalle ]1;+infi[ par f(x) = lnx - 1/lnx.
On nomme (C) la courbe représentative de f et T la courbe d'équation y = lnx dans un repère orthogonal (O;i;j).
1) Etudier les variations de la fonction f et préciser les limites en 1 et en +infi.
2)a) Déterminer la limite de [f(x) - lnx] en +infi. Interpréter graphiquement cette limite.
b) Préciser les positions relatives de (C) et de T.
3) On se propose de chercher les tangentes à la courbe (C) passant par le point O.
a) Soit a un réel appartenant à l'intervalle ]1;+infi[.
Démontrer que la tangente Ta ) (C) au point d'abscisse a passe par l'origine du repère si et seulement si f(a) - af'(a) = 0.
Soit g la fonction définie sur l'intervalle ]1;+infi[ par g(x) = f(x) - xf'(x).
b) Montrer que sur ]1;+infi[, les équations g(x) = 0 et (lnx)^3 - (lnx)² - lnx - 1 = 0 ont les mêmes solutions.
c) Après avoir étudié les variations de la fonction u définie par R par u(t) = t^3 - t² - t - 1, montrer que la fonction u s'annule une fois et une seule sur R.
d) En déduire l'existence d'une tangente unique à la courbe (C) passant par le point O.
La courbe (C) et la courbe T sont donnnées grace à la calculatrice.
Tracer cette tangente le plus précisément possible.
4) On considère une réel m et l'équation f(x)=mx d'inconnue x.
Par lecture grahique et sans justification, donner, suivant les valeurs du réel m, le nombre de solutions de cette équation appartenant à l'intervalle ]1;10].
Alors, pour ce qui est de mon travail :
1) On calcul la dérivé de f(x). Soit f'(x) = 1/x - 1/(1/X) = 1/x - x/1 = -x²/x = -x.
x étant négatif, on sait que la fonction est négative à l'extérieur des racines et positive à l'intérieur des racines.
Pour les limites: en 1 = -1 et en +infi = -infi.
2)a)lim de [f(x) - lnx] en +infi donne : lnx - 1/lnx - lnx = 1/lnx = 1/+infi = 0. C'est une asymptote horizontale.
Et puis à partir de là, je bloque complètement. Je comprend les questions, mais le problème est la résolution et surtout la méthode.
J'espère que vous pourrez m'aider.
A bientot, et merci d'avance. Kikou!
Bonjour,
1)
Ta dérivée donne bien :
f '(x)=1/x - x soit :
f '(x)=(1-x²)/x et non -x
Comme le déno x est positif, alors f ' est du signe de (1-x²) qui est positif entre les racines ( qui sont -1 et 1 ) car le coeff de x² est < 0.
Donc f ' > 0 pour x]1;+
[
et f est croissante sur cet intervalle.
lim lnx=0
x-->1
x > 1
lim 1/lnx=+ car le déno tend vers 0 par valeurs positives.
x-->1
x > 1
lim (-1/lnx)=- .
x-->1
x > 1
Par somme :
lim f(x)=- .
x-->
x > 1
lim lnx=+
x-->+
lim -1/lnx=0 car le déno tend vers +
x-->+
Par somme :
lim f(x)=+ .
x-->+
J'arrête pour l'instant.
1) Ton calcul de la dérivée f '(x) n'est pas bon.
Rappelle-toi que la dérivée d'une fonction 1/u est - u'/u².
Bonjour Priam,
j'étais parti en gym ( pour petits vieux ! ) , ce qui occupe peu l'esprit et j'ai repensé à ce pb où j'avais d'ailleurs écrit des choses parfaitement contradictoires puisque ma dérivée (fausse) était en fait négative sur ]1;+[.Et ça ne collait pas avec les limites trouvées.
Et j'ai réalisé pdt ma gym cette erreur que tu signales. Merci à toi d'avoir relu cette réponse.
Donc on rectifie pour la 1):
1/lnx est de la forme 1/u et je te cite :
la dérivée d'une fonction 1/u est - u'/u².
u=lnx donc u'=1/x
et -u'/u² donne :
Dériveé de 1/lnx est : -(1/x)/(lnx)² soit -1/[x(lnx)²]
Dériveé de -1/lnx est : 1/[x(lnx)²]
Donc f '(x)=1/x + 1/[x(lnx)²]
soit en réduisant au même déno :
f '(x)=[(lnx)²+1] / x(lnx)²
qui est tjrs positive sur l'intervalle donc f tjrs croissante.
Kikou, tu écris :
2)a)lim de [f(x) - lnx] en +infi donne : lnx - 1/lnx - lnx = 1/lnx = 1/+infi = 0. C'est une asymptote horizontale.
Sois plus précise dans ta façon d'écrire :
f(x)-lnx=lnx - 1/lnx - lnx
........= -1/lnx -->il manque un "-" aussi.
Donc :
lim [f(x)-lnx]=lim (-1/lnx)=0 car lnx tend vers +
x-->+
Donc T d'équation y=lnx est asymptote à C.
Ce n'est pas du tout une droite cette asymptote! C'est la courbe de la fonction logarithme "lnx". Uen asymptote peut-être autre chose qu'une droite. OK?
b)
On a vu que :
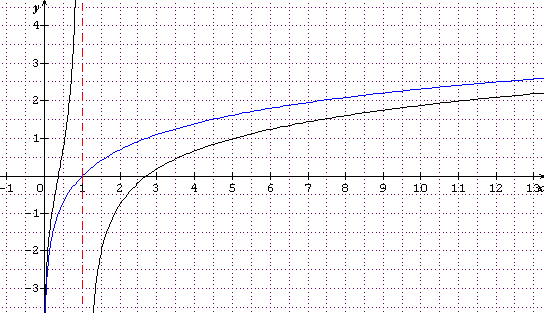
f(x)-lnx=-1/lnx
Or -1/lnx est tjrs < 0 sur ]1;+
donc :
f(x)-lnx < 0
donc :
f(x) < lnx
Donc C est sous T.
C est en noir ( Ne tiens pas compte de la partie de C située sur ]0;1[.
T est en bleu.
3)
a)
L'équa d'une tgte en un point d'abscisse "a" est :
y=f '(a)(x-a)+f(a)
ce qui donne :
y=f '(a)x -a*f '(a)+f(a)
L'ordonnée à l'origine de la tgte ( obtenue pour x=0) est donc :
-a*f '(a)+f(a)
La tangente Ta à (C) au point d'abscisse "a" passe par O si l'ordonnée à l'origine vaut zéro donc si :
-a*f '(a)+f(a)=0
ou encore :
f(a)-a*f '(a)=0
b)
g(x)=f(x)-x*f '(x)=lnx -1/lnx -x*[(lnx)²+1]/x(lnx)²
Le dernier terme est simplifiable par x qui est 
0.
g(x)=lnx -1/lnx -[(lnx)²+1]/(lnx)²
On réduit au même déno qui est (lnx)². Et on arrive, après qq. tout petis calculs, à :
g(x)=[(lnx3)-(lnx)2-lnx-1]/(lnx)2
Donc :
g(x) = 0 <===> (lnx)3- (lnx)2 - lnx - 1 = 0
3)
c)
Après avoir étudié les variations de la fonction u définie par R par u(t) = t^3 - t² - t - 1, montrer que la fonction u s'annule une fois et une seule sur R.
Tu calcules u '(t) et tu fais son tableau de variation.
Tu vois que u(t) est décroissante sur [-1/3;1] et croissante pour le reste.
Tu cherches lim en - et +
.
Tu calcules u(-1/3) et u(1).
Tu fais intervenir le TVI pour montrer que u(t) s'annule une seule fois sur [1;+
[.
d)
Donc :
(lnx)3- (lnx)2 - lnx - 1 = 0
pour une seule valeur de x
]1;+[
donc :
f(a)-a*f '(a)=0
pour une seule valeur x=a avec a
]1;+[
donc :
Il existe une tangente unique à la courbe (C) passant par le point O.
J'arrête pour l'instant.
Suite du 3) d)
La courbe (C) et la courbe T sont donnnées grace à la calculatrice.
Tracer cette tangente le plus précisément possible.
Il semble donc que tu doives tracer la courbe Cf sur ]1;15] par exemple grâce à des valeurs de f(x) ( ou y) données par ta calculatrice puis , ensuite tracer la tgte passant par O "le plus précisément possible" mais sans calculer l'abscisse du point de tangence. OK ?
Rappel :
Cf est en noir.
La tgte à Cf passant par O est en vert.
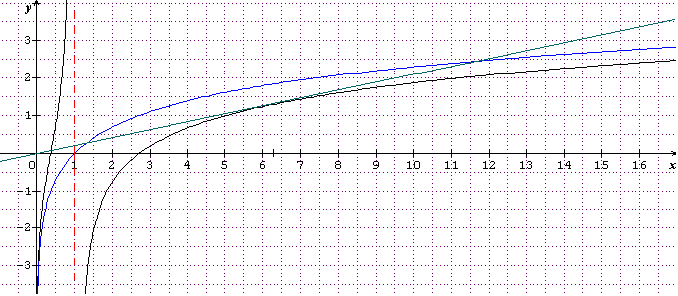
Mon graph ci-dessus est devrait être limité à x=10 environ.
4) On considère une réel m et l'équation f(x)=mx d'inconnue x.
Par lecture grahique et sans justification, donner, suivant les valeurs du réel m, le nombre de solutions de cette équation appartenant à l'intervalle ]1;10].
y=mx a pour réprésentation graphique une droite que j'appelle (d) passant par l'origine O.
f(x)=mx a pour solution l'abscisse ( ou les abscisses) des points d'intersection de (d) et de Cf.
Tu vois donc le rapport avec la tgte que l'on vient de tracer.
Si m > coeff directeur de Ta , alors ....
Etc.
Il te faut donner donner une valeur approchée du coeff directeur de la tgte Ta (en vert sur mon graph).
A+
Bonjour, et merci énormément pour toutes vos explications très claires et tout le temps que vous avez dû consacrer à m'aider.
Cependant, trois points restent sombres.
Pour la question 3)b) On a dit que g(x)=f(x)-x*f '(x) = lnx -1/lnx -x*[(lnx)²+1]/x(lnx)² = lnx - 1/lnx - [(lnx)²+1]/x(lnx)²
mais je n'arrive pas à simplifier mon calcul afin de retrouver g(x)=[(lnx^3)-(lnx)2-lnx-1]/(lnx)2
Pour la 3)c) u'(t) = 3t² - 2t - 1
t² étant toujours positif, il suffit d'étudier la fonction polynome (3t²-4t-1)
Avec delta = 16 et Racine de delta = 4.
On trouve t1 = 1 et t2 = -1/3.
D'où u'(t) < 0 pour -1/3 < x < 1.
On vois grâce au tableau de variation que u(t) est décroissante sur [-1/3;1] et croissante pour le reste.
On a donc lim de u(t) en -infi = -infi.
lim de u(t) en +infi = +infi.
u(-1/3) = -3/10
u(1) = -2
Ces quatres derniers calculs vous semble t-ils correct ?
Et comment montrer que u(t) s'annule une seule fois sur ]1;+infi[ ? Je ne sais pas vraiment comment appliquer le TVI dans notre cas.
4) Nous avons dis que f(x)=mx a pour solution l'abscisse des points d'intersection de la droite y=mx et de C.
Mais je reste bloquée là...
Merci pour votre aide, à bientot.
Bonjour,
oui, bien sûr, j'ai passé pas mal de temps sur ton pb mais j'y ai éprouvé un intérêt certain ! Je n'ai nullement sacrifié d'autres acctivités ..telle que ma séancde de gym par exemple !! Passsons aux choses sérieuses :
Pour la question 3)b) On a dit que g(x)=f(x)-x*f '(x) = lnx -1/lnx -x*[(lnx)²+1]/x(lnx)² = lnx - 1/lnx - [(lnx)²+1]/x(lnx)²
mais je n'arrive pas à simplifier mon calcul afin de retrouver g(x)=[(lnx^3)-(lnx)²-lnx-1]/(lnx)²
g(x)=f(x)-x*f '(x) = lnx -1/lnx -x*[(lnx)²+1]/x(lnx)²
Le dernier terme est simplifiable par x qui est
0.
Jusque là , tu suis ?
On arrive donc à :
g(x)= lnx -1/lnx -[(lnx)²+1]/(lnx)²
On va réduire au même déno qui est (lnx)2. Donc le dernier terme ne change pas.
g(x)=[lnx*(lnx)²/(lnx)²] -[1*lnx/(lnx)(lnx)] - [(lnx)²+1]/(lnx)²
g(x)=(lnx)3/(lnx)2-lnx/(lnx)2-[(lnx)2+1]/(lnx)2
J'ai 3 dénos (lnx)2 donc je n'en mets qu'un seul :
g(x)={(lnx)3-lnx-[(lnx)2+1]}/(lnx)2
Je supprime les [....] de -[(lnx)2+1] donc je change les signes et mes accolades deviennent des crochets:
g(x)=[(lnx)3-lnx-(lnx)2-1]/(lnx)2
J'ordonne :
g(x)=[(lnx)3-(lnx)2-lnx-1]/(lnx)2
Quand tu vas refaire sur ta feuille, cela devrait être clair ? Oui ?
Suite de tes questions :
Pour la 3)c) u'(t) = 3t² - 2t - 1
t² étant toujours positif, il suffit d'étudier la fonction polynome (3t²-4t-1)
Non, la dérivée est : u '(t)=3t²-2t-1
Et je ne comprends pas d'où tu sors ça :
t² étant toujours positif, il suffit d'étudier la fonction polynome (3t²-2t-1)
Il faut écrire :
Le coeff de t² étant positif la dérivée u '(t) est négative entre les racines du trinôme.
OK pour les racines (donc faute de frappe pour ta dérivée qui était bonne sur ta feuille).
On voit grâce au tableau de variation que u(t) est décroissante sur [-1/3;1] et croissante pour le reste.
On a donc lim de u(t) en -infi = -infi.
lim de u(t) en +infi = +infi.
OK pour tout ça.
Je suppose que tu as fait le tableau de variation et que tu as dit que la limite d'un polynôme en l'infin est donné par le limite de son terme de plus haut degré donc par la limite de t3.
u(-1/3) = -3/10
u(1) = -2
u(1)=-2 : OK
u(-1/3)=(-1/3)3-(-1/3)2-(-1/3)-1
.......=-1/27 -1/9 +1/3-1
.......=-1/27 - 3/27 + 9/27 -27/27
.......=-22/27 (
-0.8 alors que toi, tu trouves -0.3 )
Courbe de u(t) qu'il est bon de faire à la calculatrice uniquement pour vérifiaction ( et non dans le DM) :
Et comment montrer que u(t) s'annule une seule fois sur ]1;+infi[ ? Je ne sais pas vraiment comment appliquer le TVI dans notre cas.
Il faut que tu saches utiliser à peu près correctement le TVI ( les mots soulignés ci-dessous sont absolument indispensables . Pour le reste , en DS, tu fais comme tu peux pour dire l'essentiel) :
Sur ]-
;-1/3], d'après le tableau de variation , la fct u(t) est continue et srictement croissante avec :
lim u(t)=-
x-->-
et u(-1/3)=-22/27
Donc d'après le TVI, il n'existe pas de réel
sur cet intervalle tel que u()=0.
Sur [-1/3;1] , d'après le tableau de variation , la fct u(t) est continue et srictement décroissante avec :
u(-1/3)=-22/27
et u(1)=-2
Donc d'après le TVI, il n'existe pas de réel
sur cet intervalle tel que u()=0.
Sur [1;+
[ , d'après le tableau de variation , la fct u(t) est continue et srictement croissante avec :
u(1)=-2
et :
lim u(t)=+
x-->+
Donc d'après le TVI, il existe un unique réel
sur cet intervalle tel que u()=0.
Tu ne peux pas n'étudier que l'intervalle [1;+
[ car l'énoncé dit :
montrer que la fonction u s'annule une fois et une seule sur
.Donc tu es obligée d'étudier les 3 intervalles !!
4) Nous avons dis que f(x)=mx a pour solution l'abscisse des points d'intersection de la droite y=mx et de C.
Mais je reste bloquée là...
Tu comprends que donner le nb de solutions de l'équation :
f(x)=mx
c'est , en fait , trouver combien il y a de points d'intersection de la droite y=mx et de C.
C'est clair pour toi ?
Là, il faut que tu fasses pivoter ta règle (qui représente la droite y=mx) autour du point O pour voir quand elle coupe ou ne coupe pas Cf.
Mais tu restes sur ]1;10[
OK ?
Je te remets le graph où j'ai trouvé par essais successifs que la droite verte y=mx était tgte en A dont j'ai évalué les coordonnées en gros .
A(1.2;6)
Donc pour cette tgte : m=1.2/6=0.2 ( c'est une approximation).
Ma droite verte a donc pour équa : y=0.2x
Si m > 0.2 -->pas de solution à f(x)=mx ( C'est le cas de ma droite bleue dont l'équa est y=0.3x donc pour laquelle : m=0.3)
On verra la suite dans un autre graph.
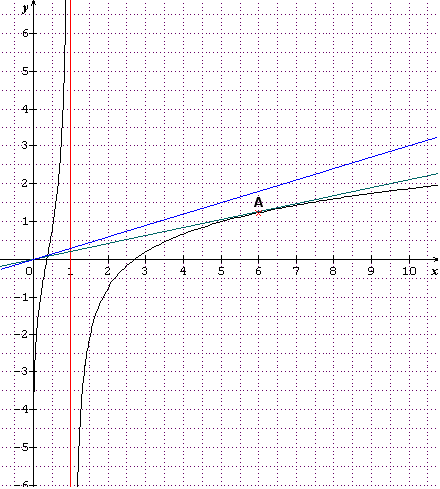
On est limité à l'intervalle : ]1;10]
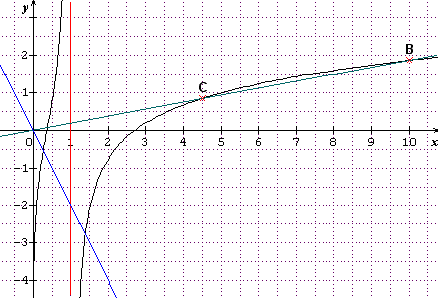
J'ai donc placé le point B(10;1.9) -->en fait le calcul donne f(10)1.87
J'ai tracé la droite (OB). Elle coupe Cf en 2 points : B et C.
Le coeff directeur de la droite (OB) est donc , en gros : 1.9/10=0.19
Si 0.19 
m < 0.2 , alors f(x)=mx a 2 solutions .
Si m < 0.19 , alors f(x)=mx a une seule solution. ( Cas de ma droite bleue où j'ai choisi m=-2).
Bonne continuation et je n'aurai probablement plus l'occasion de t'aider car je ne fais pas les pbs de TS ( enfin celui-là me plaisait bien !!).
bonjour à tous! j'ai un DM à rendre pour demain,j'aimerai avoir de l'aide pour la dernière question de la PARTIE B s'il vous plait voilà jespère que quelqu'un pourra m'aider rapidemment.
voilà l'énoncé de l'exercice:
* Tom_Pascal > Kikou7 aucun rapport avec le topic en cours, si tu veux de l'aide, merci de poser ton exercice dans un nouveau topic (une seule fois). Lis les règles du forum pour en comprendre son fonctionnement STP. *
Annuler
connectez vous