Inscription / Connexion Nouveau Sujet
Fonction logarithme népérien Terminale ES
Bonjour, j'ai cet exercice de maths à faire mais j'ai quelques difficultés. Pouvez m'aidez s'il vous plait?
Soit la fonction f définie et dérivable sur l'intervalle ]-0.5;+oo[ par :
f(x)=-x²+2x-ln(2x+1).
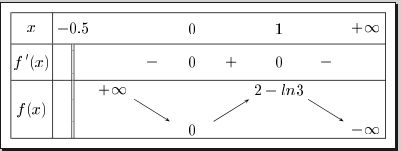
1) Déterminer le tableau de variations complet (ensemble de définition, signe de la dérivée, variations de f et limites aux bornes de son ensemble).
2)a) Déterminer le nombre de solutions de l'équation f(x) = 0 sur l'intervalle [0.5; +oo[.
b)Donner un encadrement d'amplitude 10^-2 de chacunes de ces solutions.
3)Etudier le sens de variation d'une fonction F, primitive de f sur l'intervalle ]0.5; +oo[
En fait, je bloque pour la première question, d'une part parce que je n'arrive pas à dériver la fonction f.
Merci d'avance.
Bonjour,
qu'est ce que tu n'arrive pas à dériver ? le ln (2x+1) ? c'est du type ln(u) et la dérivée est u'/u
Oui, c'est ca qui me géne.
Si je fais comme ca ca me donne :
f'(x) = -2x+2- (2/2x+1)
et je trouve au final :
f'(x) = -2x/(2x+1)
C'est juste ?
jusqu'à f'(x) = -2x+2- (2/2x+1) je suis d'accord mais c'est pas avec f'(x)=-2x/(2x+1) tu peux essayer de mettre au même dénominateur pour continuer :
donc tu pars de et tu mets au même dénominateur.
Pour la limite en +oo, on peut dire que c'est la limite du terme de plus haut degré même s'il y a la fonction logarithme ?
Parfait, j'ai trouvé que la limite de f(x) quand x tend vers -0.5 est de +oo et -oo quand x tend vers +oo. 
Je demandais ca :" Pour la limite en +oo, on peut dire que c'est la limite du terme de plus haut degré même s'il y a la fonction logarithme ? "
pour la rédaction.
Pour la 2) a) je trouve grace au tableau de variations que f(x) = 0 n'a qu'une seule solution qui appartient à l'intervalle [0,5;+oo[. En même temps c'est logique lorsqu'on a le tableau de variations.
Pour la question 2) b) je vais conjecturer à la calculatrice. Je trouve que la solution : 0.81 < 
< 0.82.
non si on avait eu 
- on aurait dû utiliser la croissance comparée, je ne sais pas si vous avez vu ça en cours pour la rédaction tu peux rédiger comme ça :
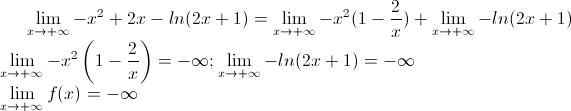
Pour le signe de la dérivée j'ai fais :
pour tout x 
]-0.5;+oo[, 2x+1 > 0 . Donc f'(x) est du signe de a, sachant que 
= 4 et les racines sont 0 et 0,5. Ce sera du signe de a à l'extérieur des racines et du signe contraire à l'interieur.
Donc f'(x) > 0 
x [0;0,5].
Non, on nous dit seulement que :
3)Etudier le sens de variation d'une fonction F, primitive de f sur l'intervalle ]0.5; +oo[
il faut que tu fasses un tableau de signes sur ]-0.5;+[,
étudier le signe de -x²+2x=x(2-x)
étudier le signe de 2x+1
déterminer le signe de -x²+2x/2x+1
C'est bizarre mais on n'a vraiment jamais vu la primitive d'une fonction ln. Je demanderais au prof.
En tout cas merci de ton aide !
Bonne soirée.
J'ai déjà répondu plus haut.
"Pour la 2) a) je trouve grace au tableau de variations que f(x) = 0 n'a qu'une seule solution qui appartient à l'intervalle [0,5;+oo[. En même temps c'est logique lorsqu'on a le tableau de variations.
Pour la question 2) b) je vais conjecturer à la calculatrice. Je trouve que la solution : 0.81 < < 0.82."
Annuler
connectez vous