Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale DérivéesTopics traitant de Dérivées [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Fonction terminale

Posté par
ratab 24-01-21 à 10:21

Bonjour,

Soit la fonction f définie sur R par 𝑓(𝑥) = (2 − 𝑥)e (exposant x)

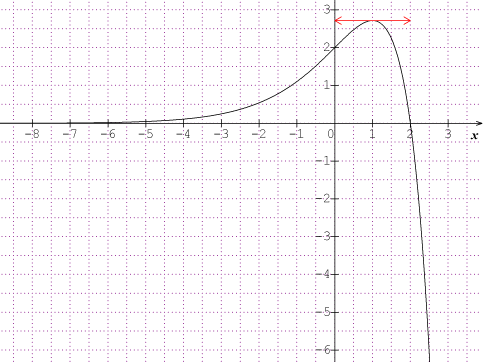
1) Faire l'étude complète de la fonction 𝑓.
2) Etudier la convexité de la fonction 𝑓 et préciser s'il existe un point d'inflexion.
3) Déterminer l'équation de la tangente à la courbe Cf au point d'abscisse 2.

Merci d'avance

Posté par
heklare : Fonction terminale 24-01-21 à 10:24

Bonjour

Que proposez-vous ? Qu'est-ce qui vous gêne ?

Posté par
matheuxmatoure : Fonction terminale 24-01-21 à 10:24

bonjour

on attend tes propositions !

Posté par
matheuxmatoure : Fonction terminale 24-01-21 à 10:25

(bonjour hekla... posts croisés, je te laisse )

Posté par
Tilk_11 Moderateurre : Fonction terminale 24-01-21 à 10:27

Bonjour ratab,
je vois que tu es nouveau sur l', bienvenue à toi.
Tu as certainement lu Sujet ancien- ne plus donner ce lien-merci

Quelles sont tes pistes de recherche ? (point n°4)

Posté par
heklare : Fonction terminale 24-01-21 à 10:28

Bonjour matheuxmatou

d'accord  je vous laisse l'autre sujet

Posté par
ratabre : Fonction terminale 24-01-21 à 10:53

Bonjour,

Je suis désolée de ne pas avoir mis de proposition.
J'ai essayé de le faire mais je suis bloqué au debut, voici ce que j'ai commencé à faire.

f(x)= (2-x)e(exposant x)    
u= 2-x     u'= -1
v=e(exposant x)    v'= e(exposant x)
f'(x) = u' * v + u * v'
          = -1 * e(exposant x) + (2-x) * e(exposant x)
          = - e (exposant x) + 2e(exposant x) - e (exposant 2x)
          = e(exposant x) - e(exposant x)x

Posté par
heklare : Fonction terminale 24-01-21 à 11:06

pour les exposants utilisez au moins ^  AltGr9

f(x)=(2-x)\text{e}^x

f'(x)= -\text{e}^x+(2-x)\text{e}^x

f'(x)=\text{e}^x(1-x)

Oui  

Signe de f'(x)  ?

Posté par
ratabre : Fonction terminale 24-01-21 à 11:09

Merci pour l'aide.
fc(x) positive car e^x > 0

Posté par
ratabre : Fonction terminale 24-01-21 à 11:10

f'(x)*

Posté par
heklare : Fonction terminale 24-01-21 à 11:13

Sous la forme factorisée il est manifeste que f'(x) n'est pas toujours positive

Posté par
ratabre : Fonction terminale 24-01-21 à 11:15

Du coup le tableau de variation avec les limites ça serait ça ?

Fonction terminale

**image recadrée**

Posté par
ratabre : Fonction terminale 24-01-21 à 11:17

Du coup f'(x) négative ?
Donc le tableau de variation serait pareil sauf que c est négatif et la droite que j'ai faite devrait être en descendant

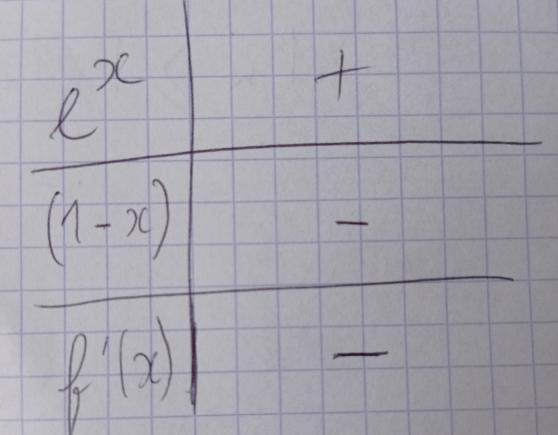
Fonction terminale

Posté par
heklare : Fonction terminale 24-01-21 à 11:21

Quel est le signe d'un produit ?

Pour tout x \in \R, \text{e}^x >0

Qu'en est-il de 1-x ?

Posté par
ratabre : Fonction terminale 24-01-21 à 11:22

Ça dépend si x est positif ou négatif non?
Du coup on peut pas savoir

Posté par
heklare : Fonction terminale 24-01-21 à 11:24

Revoir les limites

-\times +=-  (pour +\infty)

Posté par
heklare : Fonction terminale 24-01-21 à 11:24

Vous savez bien résoudre 1-x>0

Posté par
ratabre : Fonction terminale 24-01-21 à 11:26

Oui, et pour - infini : - × - = - infini

Posté par
ratabre : Fonction terminale 24-01-21 à 11:28

1 - x > 0
1 > x
Donc x positif donc 1-x négatif ?

Posté par
heklare : Fonction terminale 24-01-21 à 11:30

??????

donc si x<1,\  1-x >0 par conséquent  f'(x) >0

complétez puis variation

Posté par
ratabre : Fonction terminale 24-01-21 à 11:32

Aaaaaah okay j'ai compris, merci
Je vais essayer de faire la suite

Posté par
heklare : Fonction terminale 24-01-21 à 11:53

Les variations  ne devraient pas poser de problème

Posté par
ratabre : Fonction terminale 24-01-21 à 11:58

Voici les limites.
Donc la l'étude complète de la fonction est finie.
Par contre je ne comprends la question 2 qu'est ce que je dois faire. C est quoi convexité et inflexion?

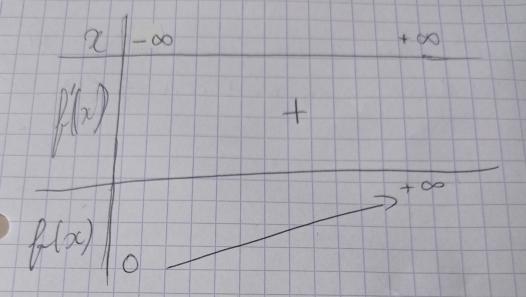
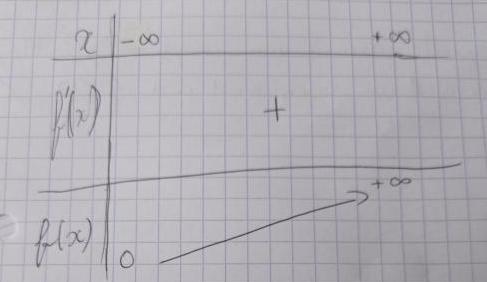
Fonction terminale

Posté par
heklare : Fonction terminale 24-01-21 à 12:04

Que faites -vous de 1  ?

Pour la limite en +\infty   je vous ai rappelé la règle des signes.

Posté par
ratabre : Fonction terminale 24-01-21 à 12:08

Le 1 ne change pas les limites non?

Fonction terminale

Posté par
heklare : Fonction terminale 24-01-21 à 12:14

Non mais en 1 le signe de la dérivée change

  Une illustration de la courbe

Fonction terminale

Posté par
ratabre : Fonction terminale 24-01-21 à 12:45

Voici le tableau de variation.
Mais quand je fais f(1) je ne trouve pas un chiffre , donc je dois mettre 3e^1 dans le tableau ?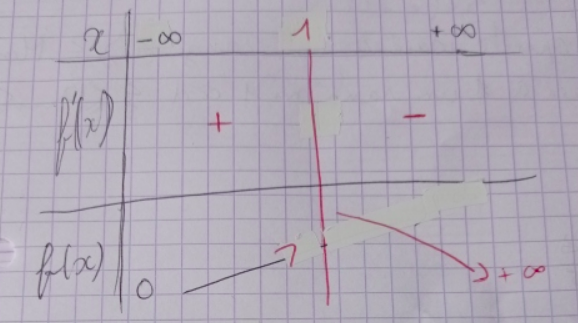
Fonction terminale

Posté par
heklare : Fonction terminale 24-01-21 à 12:50

Non  pour la limite en +\infty


+\infty\times (-\infty)=-\infty


\text{e} est bien un nombre réel   certes ce n'est pas un entier

Posté par
ratabre : Fonction terminale 24-01-21 à 12:54

Okay merci 👍
Par contre pour la question 2 je ne comprends ce qu'ils me demandent car je ne vois pas c est quoi convexité et inflexion

Posté par
heklare : Fonction terminale 24-01-21 à 13:01

Vous avez bien une définition

f est convexe sur I,  si pour tout x\in I\  f''(x)>0

Posté par
malou Webmasterre : Fonction terminale 24-01-21 à 15:03

Bonjour à vous deux
ratab, relis moi un peu ça s'il te plaît...je vois des images interdites là...

attentionextrait de c_faq la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Posté par
malou Webmasterre : Fonction terminale 24-01-21 à 15:06

ratab @ 24-01-2021 à 12:54

Okay merci 👍
Par contre pour la question 2 je ne comprends ce qu'ils me demandent car je ne vois pas c est quoi convexité et inflexion

Fonction convexe, concave et point d'inflexion


Rechercher
Menu
Espace membre
12 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !