Inscription / Connexion Nouveau Sujet
Fonctions
Bonjour, je dois faire cet exercice pour la rentrée quelqu'un pourrait m'aider svp?
1) Verifier la fonction F définie sur [0;3] par F(t) = -20e (-t²/2) est une primitive de f [0;3]
2) Déduire l'aire du domaine plan limité par l'axe des abscisses, la courbe Cf et les droites d'équation t=0 et t=3, exprimée en unités d'aire, puis cm².
3) Quelle est la valeur moyenne de f sur [0;3]?
4) Quelle a été la somme totale transférée à la fin des 3 minutes? (à l'euro près)
Merci d'avance
Bonjour, oui pardon
f se définie par f(t) = 20t e(-t²/2)
où t est le temps exprimé en min et f(t) est la vitesse instantanée d'un flux financier que l'on peut supposer continu et dont la vitesse instantanée a été variable en fonction du temps.
La somme totale = Vitesse pendant les 3 minutes d'ouverture du site par la fonction f
Bon, tu dérives F et tu dois trouver f.
L'aire est donnée par la valeur moyenne est cette aire divisée par 3. On a du te donner quelque part une indication sur la correspondance entre unité d'aire et cm carré.
tant que tu n'auras pas mis un énoncé complet ce sera un dialogue de sourds! Comment veux-tu que je devine d'où sort ce 0,64?
Oui je comprends, mais ce 0.64 vient d'une règle générale
Pour passer d'1 u.a à 1 cm², il faut multiplier par 0.64 à ma connaissance
Après peut-être que je me trompe, je ne suis pas ce qu'on appelle un ''matheux'' désolé ..
Une société d'achats en ligne veut analyser le déroulement d'une ventre promotionnelle ''flash'' qu'elle a organisée sur internet.
Cette vente, d'une durée annoncée de trois minutes, a provoqué sur son site un flux financier que l'on peut supposer continu et dont la vitesse pendant les trois minutes de l'ouverture du site par la fonction f définie La Fonction f définie par f(t) = 20t * e (-t²/2)
t = le temps exprimé en minutes
(t appartient à l'intervalle [0;3]) et f (t) = la vitesse instantanée d'un flux, exprimé en milliers d'euros par minute.
Arrondi au millième près
1) Faire la dérivée de f
En déduire le sens de variation de f sur [0;3]
2) Démontrer que la vitesse admet un maximum. (arrondi au millième près)
3) Dessiner la courbe représentant Cf de f dans un repère orthogonal (5cm en abscisse, 1cm en ordonnée) et préciser la tangente de Cf au point d'abscisse 0 (calculer son coeff directeur)
C'est la première partie .
Ensuite je vous ai donné le reste ..
je ne sais pas de quel 0,64 tu parles... mais ici on te donne l'echelle... 5cm en abscisse et 1cm en ordonnée!
Bon, tu as fait la courbe?
D'accord, et bien dites moi quelle échelle et je vous l'aurais donnée directement ..
Non, je n'ai pas su faire le 2)
Bien... Comme une exponentielle est positive, pour avoir le signe de f' il suffit de connaitre celui de sur [0;3]. Alors? ça s'annule quand?
Oui comme l'exponentielle est toujours positive, f est croissante sur [0;3]
1-t² sur [0;3] s'annule lorsque t = 1
Donc 1 est la valeur interdite c'est ça?
Non, 1 est la valeur ou f a un extremum, qui ici est un maximum parce que c'est positif avant et négatif après. Le maxmum vaut donc
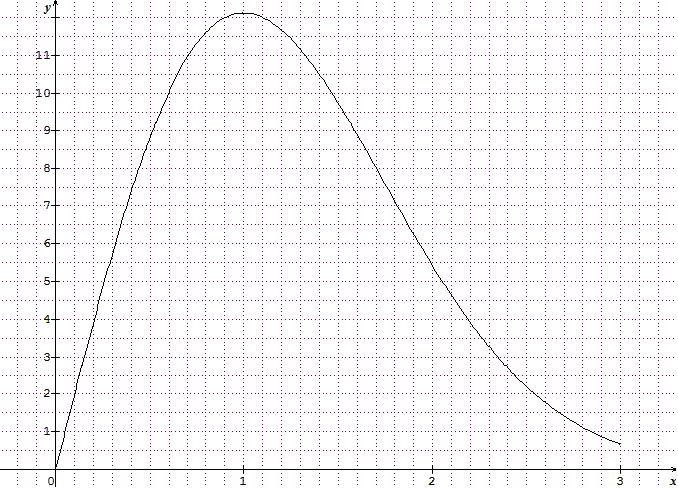
D'accord donc c'est décroissant et croissante ensuite , le changement de signe ''se fait'' à x = 1
La tangente de Cf au point d'abscisse 0 il faut appliquer la formule :
f'(a) (x-a) + f (a)
C'est cela?

 de quoi tu parles?
de quoi tu parles?
