Inscription / Connexion Nouveau Sujet
Fonctions
Bonjour j'ai vraiment du mal à faire cette exercice. Je l'ai commence. Je ne sais pas si ce que j'ai fait est juste. Vous pouvez m'aider s'il vous plait. Merci d'avance.
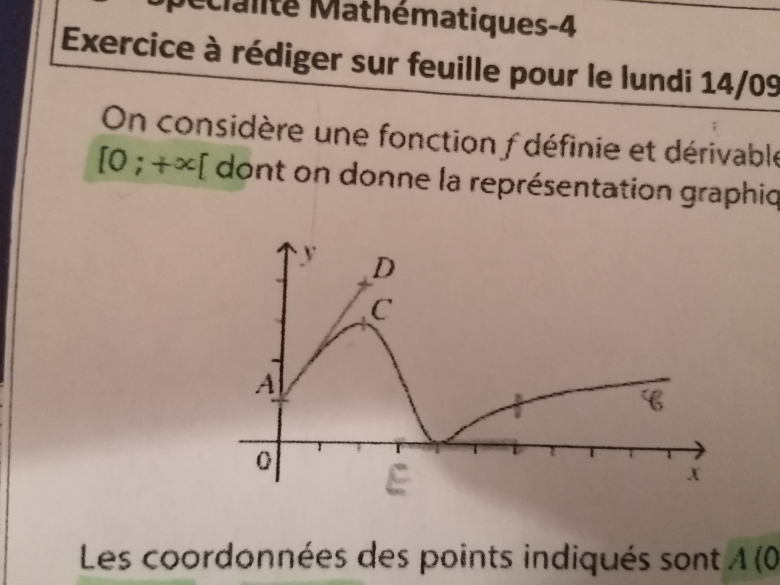
On considère une fonction f définie et dérivable sur [0;+ infini[ dont on donne la représentation graphique.
Les coordonnées des points indiqués sont A(0;1) ,D(2;4) et C (2;3).
La droite (AD) est tangente à la courbe au point d'abscisse 0.
La courbe rencontre l'axe des abscisses au point d'abscisse 4.
On sait que f(6)=1 et que la tangente au point d'abscisse 6 passe par le point E(3;0).
1 Par lecture graphique et justifier
a déterminer f(0), f'(0) et f'(6)
f(0)= 1
Je suis allée sur le point d'abscisse 0 et j'ai remonté jusqu'à la courbe et j'ai trouvé 1.
f'(0) =1.5
J'ai utilisé la formule yb-ya/xb-xa et les coordonnées de la tangente (AD).
donc yb-ya/xb-xa=4-1/2-0=3/2=1.5
f'(6)=0
On sait que f(6)=1 et que la tangente au point d'abscisse 6 passe par le point E(3;0)
Donc j'en ai déduit la tangente. Cette droite horizontale, son coefficient directeur est nul donc f'(6)=0
b déterminer une équation de la tangente à la courbe au point d'abscisse 6
On utilise l'équation de la tangente
f(a)+f'(a) (x-a)
f(6)+f'(6) (x-a)
6+0(x-0) =6
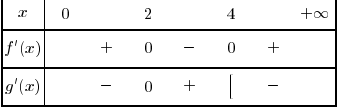
c dresser le tableau de signes de f'
x 0 6 +infini
f' - +
2 On considère la fonction g définie par g=1/f
a déterminer le domaine de définition de g
b donner l'expression de g' à l'aide de f et de f'
c en déduire le sens de variation de g
Pour f(0) même pas besoin on vous dit que la courbe passe par A (0;1) donc f(0)=1
(AD)
Tangente en 6
Donnez un nom au point d'abscisse 6 ce sera plus facile pour la rédaction
Il ne semble pas que la tangente au point d'abscisse 6 soit parallèle à l'axe des abscisses
fonction croissante courbe montante dérivée positive
fonction décroissante courbe descendante dérivée négative
revoir votre tableau
Pour 2 que proposez-vous ?
pour la 2 je propose:
a) le domaine de définition de g est ]0;+infini[
b) g= 1/f
g' = 1/f^2
c)
je ne suis pas sur
Il me semble que la courbe passe par le point de coordonnées (nommer les points)
par conséquent ne peut être définie en 4 mais elle est parfaitement définie en 0
Reprendre le tableau de signe de , vous en déduisez alors le signe de
puis le sens de variation de
le tableau de signe de f' est positif , j'en déduis que le signe g' est negatif vu que la derivée est negatif et le sens de variation décroissant
Ce n'est pas ce que je trouve
De A à C la courbe « monte » donc la fonction est croissante sur et par conséquent la dérivée est positive
De C à F la courbe « descend » donc la fonction est décroissante sur et par conséquent la dérivée est négative
Après F la courbe « monte » donc la fonction est croissante sur [0~;~2] et par conséquent la dérivée est positive
d'où le tableau précédent 11 : 49
Il ne s'agit pas du sens de variation mais du signe de la dérivée
Oui c'est bien ce que j'ai écrit dans le tableau 11 : 49