Inscription / Connexion Nouveau Sujet
Fonctions dérivée et tangente
Bonjour !
Je m'excuse encore de vous déranger. J'ai un devoir de mathématiques à rendre et j'ai cruellement besoin de votre aide : je n'arrive pas du tout à résoudre ce problème. Je suis en première spé et c'est sur les dérivations !
Voici l'énoncé :
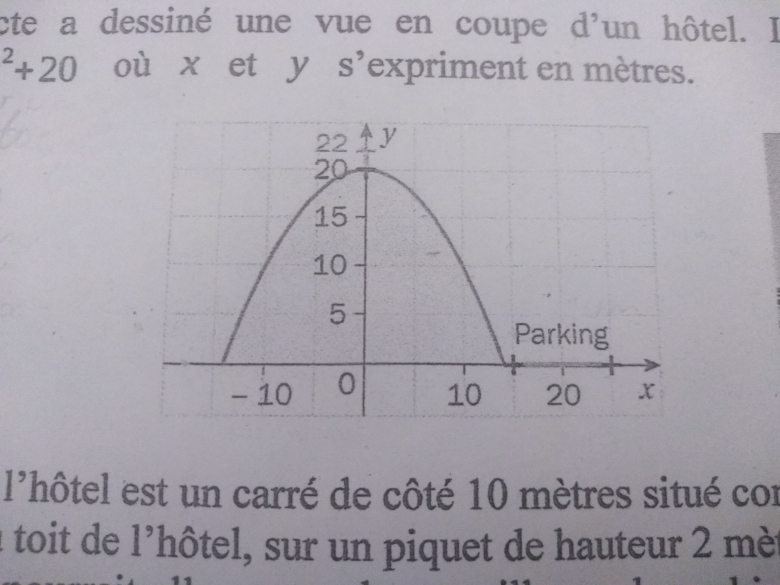
"Un architecte a dessiné une vue en coupe d'un hôtel. Il est représenté par une parabole d'équation
[y = - 0.1x^2 + 20
où x et y s'expriment en mètres.
Le parking de l'hôtel est un carré de 10 mètres situé à côté sur la vue en coupe ci-dessus. Au sommet du toit de l'hôtel, sur un piquet de hauteur de 2 mètres, il est prévu d'installer une webcam. Cette webcam pourrait-elle assurer la surveillance du parking? Expliquez le raisonnement. "
L'image que j'ai joint est le graphique qu'on a dans l'exercice.
Ayant beaucoup de difficultés à comprendre ce qu'on attend de moi lors des problèmes (je préfère quand c'est bien clair haha..), j'ai beaucoup de mal à comprendre cet exercice. Je suis d'habitude assez fort en derivation, mais là..
Je pense qu'il faut trouver l'équation d'une tangente de façon à ce qu'elle passe dans le "périmètre" du parking.. On sait déjà que il faut que l'ordonnée à l'origine de la tangente soit 22. Mais mise à part ça, je n'arrive clairement pas à résoudre cet exercice..
Pouvez-vous m'aider s'il vous plaît?
bonjour
ton intuition est la bonne.
il faut chercher s'il existe un point M de la courbe, d'abscisse a,
tel que la tangente à la courbe en ce point, passe par les points A(0;22) - la webcam - et le point B(?;?) qui représente l'extrémité du parking.
Dans un premier temps, comment déterminer les coordonnées de B ?
je rectifie :
... que la tangente à la courbe en ce point, passe par les points A(0;22) - la webcam -
et par, ou au-delà du point B(?;?) qui représente l'extrémité du parking.
Bonjour !
Merci de votre réponse!!
En sachant que le point B se situe sur la parabole, je suppose qu'il faudrait seulement lire graphiquement ses coordonnées, non ? On trouve B(15;0)
Je ne saurai pas trouver d'autres manières de déterminer les coordonées du point B sans passer par le graphique, à vrai dire je pense qu'il faudrait faire usage du paramétrer que le parking est de côté 10 mètres..?
non, le point B n'est pas sur la parabole :
B est en bordure du parking, soit à 10 m du pied H de l'hôtel.
tu peux calculer l'abscisse de H, et en déduire celle de B.
ps : dès le départ, remarquer que l'axe des ordonnées est axe de symétrie de la parabole (à justifier...),
et donc ce qui se passera sur la moitié "droite" de la parabole, sera également valable, par symétrie, du coté "gauche".
tu sais poursuivre ?
je pense oui, j'ai fait ceci :
On calcule l'abscisse du point H de la parabole tel que y=-0,1x^2+20
On a H(?;0) -> (X;f(X)) et f(X)= 0
On résout l'inequation : y=-0,1x^2+20=0
y=-0,1x^2 +20-20 = -20
y = -0,1x^2/-0,1 = -20/-0,1
y = x^2 = √200
y= x= 10√2
Les coordonnés du point H sont H(10√2;0)
Après cela, on a seulement à rajouter 10 dans mes résultats pour trouver les coordonnées du point B? (en espérant que je ne me suis déjà pas trompé  )
)
des imperfections à reprendre.
H(xH ; 0)
On cherche l'abscisse du point H de la parabole tel que -0,1xH^2+20=0
On résout l'équation : f(x)=0 soit --- une inéquation, c'est lorsqu'il y a une inégalité
-0,1x² +20 = 0 --- un seul et unique signe = dans une équation
-0,1x² +20-20 = -20
-0,1x²/-0,1 = -20/-0,1
x^2 = 200
x= -  200 ou x = +
200 ou x = + 200 ==> 2 racines !
200 ==> 2 racines !
x = -10 2 ou x = 10
2 ou x = 10 2
2
De part la symétrie de la courbe, on choisit, par exemple, l'abscisse positive.
Les coordonnés du point H sont H(10 2;0)
2;0)
Après cela, on a seulement à rajouter 10 dans mes résultats pour trouver les coordonnées du point B? ---- oui
donc B(10 2 + 10 ; 0)
2 + 10 ; 0)
ensuite, pour la tangente en a, comment comptes-tu t'y prendre ?
Merci pour avoir réglé mes imperfections !
Pour la tangente en a, je comptais au départ (parce que j'avais déjà essayé de faire cet exercice sans aide) de calculer la dérivée de y = -0,1x^2+20 pour ainsi déterminer l'équation de la tangente (ta:y=mx +p puisque la tangente est une droite affine.. et que on sait déjà l'ordonnée à l'origine qui est 22 et mx= f'(X))
Le problème étant que maintenant que nous avons trouvés les coordonnées de H et de B, je suppose qu'il faut en faire usage, d'autant plus si on veut trouver le point d'abscisse a que je ne peux pas trouver sauf graphiquement..
À vrai dire, à ce niveau, je saurai pas comment faire..
pour le moment, on garde les coordonnées de B sous le coude, on s'en servira lorsque tu auras établi l'équation de la tangente en a.
pars de l'équation générale d'une tangente (celle du cours)
Ta : y = f '(a)(x-a) + f(a) --- "a" restera "a" dans tes calculs
ceci fait, on veut que le point (0;22) appartienne à Ta... petite équation à résoudre pour en déduire la valeur de a,
et donc l'équation définitive de la tangente.
restera enfin à chercher le point d'intersection entre cette tangente et (Ox)
pour savoir si B sera "couvert" par la webcam, ou pas.
Excusez-moi de la réponse tardive.. Je viens de faire l'équation de la tangente et j'ai trouvé (inutile d'encombrer la conversation avec mes détails calculatoires très rigoureux..)
Ta : y= f'(0)(x-0)+f(0)
Ta : y= 20(x-0)+22
Ta : y= 20x+22
Je m'apprête de ce pas à faire la suite (que vous m'avez gentiment indiqué !) mais j'ai du mal à comprendre, qu'estce que "(Ox)"?
ce que tu as fait n'est pas ce que j'attendais.
tu as essayé d'établir la tangente en 0, et non pas en "a".
par ailleurs, cette équation (même en 0) est fausse.
normalement, en 0, il y a une tangente "horizontale", donc de la forme y=p, pas y=mx+p.
...montre quelle dérivée f '(x) tu as trouvée,
je remets mon message précédent :
pars de l'équation générale d'une tangente (celle du cours)
Ta : y = f '(a)(x-a) + f(a) --- "a" restera "a" dans tes calculs
et (Ox), c'est l'axe des abscisses.
ah ! désolé pour cette faute !! j'avais la tête en l'air..
j'ai du coup refait le calcul de l'équation de la tangente et j'ai trouvé ceci (je bloque un peu sur la fin, d'ailleurs)
pour f'(a) j'ai trouvé comme résultat (après avoir fait lim f'(a) lorsque a tend vers h...) -0,2a.
Puis j'ai fait l'équation de la tangente :
Ta: y= -0,2a(x-a) + (-0,1a²+20)
Ta: y= -0,2ax+0,2a²+(-0,1a²+20)
Je doute de ce résultat (et je me vois d'ailleurs confus par le "(-0,1a²+20)" à la fin
pour f'(a) j'ai trouvé comme résultat (après avoir fait lim f'(a) lorsque a tend vers h...)
ah ? tu n'as pas utilisé les formules de dérivation vues en cours ?
f(x) = - 0.1x² + 20
f '(x) = 2 * (-0.1) * x + 0 = -0.2x --- et hop terminé !
donc f '(a) = -0,2a --- exact
équation de la tangente en a :
Ta: y= -0,2a(x-a) + (-0,1a²+20)
Ta: y= -0,2ax+0,2a²+(-0,1a²+20) --- on peut réduire ça
Ta: y= -0,2ax+0,1a² +20 ok
à partir de là, tu sais que A(0;22) doit appartenir à cette tangente
pose l'équation en a qui traduit cette condition, et résous-là.
Ma démarche est la suivante (pour la réponse du dessus)
Ta : y=f'(a)(x-a)+f(a)
avec f'(a)=f(a+h)-f(a)/h
et f(a+h)= -0,1(a+h)²+20 = -0,1(a²+2ah+h²)+20 = -0,1a²-0,2ah-0,1h²+20
et f(a)=-0,1a²+20
donc f'(a)=-0,1a²-0,2ah-0,1h²+20-(-0,1a²+20)/h
=-0,1a²-0,2ah-0,1h²+20+0,1a²-20/j'
=-0,2ah-0,1h²/h
= -0,2a-0,1h
lim f'(a) lorsque h->0 = -0,2a-0,1xh = -0,2a
Pour l'équation de la tangente,j'ai montré ma démarche au dessus
oui oui, j'avais bien compris que tu avais fait ainsi.
ce que je disais, c'est que ce type de calculs, on le fait quand on "découvre" la notion de dérivée en cours.
ensuite, le professeur donne un formulaire pour dériver rapidement les fonctions usuelles.
dans ce style : ![]() Formules - Formulaire : Dérivées de fonctions usuelles
Formules - Formulaire : Dérivées de fonctions usuelles
mais si tu ne l'as pas dans le cours, ta façon de faire était la bonne.
" ta façon de faire était la bonne."
enfin presque, à lecture plus attentive, je vois de petites erreurs
ah! Il est vrai que je n'ai pas utilisé les fonctions usuelles..
Équation de la tangente tel que A(0;22) appartient à la tangente ;
y= -0,2×0x+0,1×0²+20
:y= 20?
Je n'y arrive vraiment pas à ce niveau, je m'excuse..
y= -0,2a x +0,1a² +20
si le point A(0;22)  Ta alors ses coordonnées vérifient l'équation.
Ta alors ses coordonnées vérifient l'équation.
x prend quelle valeur dans l'équation ?
y prend quelle valeur ?
l'équation devient ...?
(et "a" reste "a" , c'est ton inconnue ! )
je pense avoir compris !
On veut que A(0;22) appartienne à Ta
Donc y=-0,2ax+0,1²+20
avec y=22 et a=0
donc 22=-0,2a×0+0,1²+20
mais du coup, vu que l'inconnu part (on aurait 22=0,1²+20 donc a serait parti), ce serait donc impossible? Où je me trompe?
déjà dit (2 fois ^^) que a est ton inconnue.
pourquoi tiens-tu tant à la mettre à 0??
x=0 et y=22
y= -0,2a x +0,1a² +20 devient 0,1a² +20 = 22
d'accord ?
d'accord,j'avais oublié le a du "+0,1a²"
donc :
22=0,1a²+20
22-20=0,1a²
2/0,1=0,1a²/0,1
a²=√20
a=2√5
C'est bon?
euh... presque
attention, tu as fait la mm erreur que tout à l'heure.
a²=√20
a= - 2√5 OU a= + 2√5 ---- 2 solutions
comme on a décidé de travailler sur la portion de parabole avec les x positifs (en choisissant l'abscisse positive pour H),
la solution à retenir est a = 2√5
et donc, l'équation de Ta devient ...?
pour la suite tu as une petiteidée ?
fais un dessin à main levée pour repositionner le problème,
ou bien trace la tangente (à peu près aussi) sur le graphique de l'énoncé.
ton dernier message me met le doute sur ta bonne compréhension du fameux "a".
d'où un petit dessin... enfin pas trop petit pour que tu puisses voir le point B, entre autres.... 
"a" est l'abscisse du point M, point de tangence à la courbe,
tel que la tangente en M passe par le point A.
merci encore !
du coup l'équation Ta, j'ai fait ceci mais je pense clairement que c'est faux : f'(2√5)(x-2√5)+f(2√5)
avec f'(2√5)=-0,2x2√5
et f(2√5)=-0,1²x(2√5)²+20=18
donc Ta : y=(-0,2x2√5)(x-2√5)+18
y=(-0,2x2√5)+14.
Cependant ce résultat ne fait aucun sens,puisque le coefficient directeur si Ta passe par A doit être de 22??
D'autant plus que mon raisonnement est idiot ; je ne fais que de tourner en rond..
En ce qui concerne la suite, j'ai déjà tracé ma tangente et d'un point de vu graphique, on peut déjà voir que la tangente qui passe par le point A et touche en un point de la courbe d'abscisse a bien après le point B (10√2;0), donc la caméra ne pourra pas assurer la surveillance du parking..
alors...
la première partie de ton message est truffé de petites sottises 
je détaille, on est là pour apprendre !
1) pourquoi ré-établir Ta ?
tu avais trouvé Ta: y= -0,2ax+0,1a² +20 ---- on remplace a par 2 5 et c'est tout, pas besoin de tout refaire.
5 et c'est tout, pas besoin de tout refaire.
y= -0,2*2 5 x+0,1 (2
5 x+0,1 (2 5 )² +20
5 )² +20
y= ... à réduire
2) tu as trouvé ceci : y=(-0,2x2√5)+14. C'est faux, mais je reprends les détails :
- pourquoi ne pas réduire encore ? -0,2*2 = -0.4
- dans cette équation, tu trouves 14 pour ordonnée à l'origine... pas cohérent avec le point A...
3)" le coefficient directeur si Ta passe par A doit être de 22"
attention, tu confonds ordonnée à l'origine et coefficient directeur.
==> le coeff. directeur, c'est la pente de la droite :
dans le cas présent (voir dessin), on voit que la tangente 'descend', donc on doit trouver une pente négative.
comprends-tu bien tous ces points (... sont importants) ?
concernant la fin de ton message, tu as bien compris, mais il faut le démontrer !
- calculer l'abscisse du point d'intersection (le point C sur mon dessin),
- comparer ensuite avec l'abscisse de B (déjà trouvée)
- et conclure.
je n'avais pas vu ceci : "donc la caméra ne pourra pas assurer la surveillance du parking.."
tu en es sûr ?
D'accord, merci pour ces explications et le graphique au passage, je comprends bien mieux ! (surtout que vous donne du fil à retordre au vu de ma compréhension!)
Pour réduire sur l'équation de la tangente :
On remplace : Ta: y=(-0,2x2√5)X+0,1x(2√5)²+20
y=(-0,2x2√5)+22
L'équation de la tangente est donc ------
Pour trouver l'abscisse de C:
On a C(Fx ;0) avec Fx=?
On résout l'équation f(X)=0 :
(-0,2x2√5)x+22=0
(-0,2x2√5)X+22-22=-22
(-0,2x2√5)X/(-0,2x2√5)=-22/(-0,2x2√5)
X=-22/(-0,2x2√5)
donc C(-22/(-0,2x2√5);0)
or on remarque que C(-22/(-0,2x2√5);0) > B(10√2+10;0)
donc la tangente Ta --vision de la webcam -- ne passe pas par le point B ou au-deçà de celui-ci
donc la webcam ne pourra pas assurer la surveillance du parking!!
T : y= -0.4√5 + 22 oui
note : on trouve un coeff. directeur négatif, et l'ordonnée à l'origine 22.
donc tout va bien 
Pour trouver l'abscisse de C(x ;0) , on résout l'équation f(x)=0 oui
...
x =-22/(-0.4√5) ---- pense à calculer/réduire chaque fois que c'est possible
x = 55/√5
x  24.60 m
24.60 m
or on remarque que C(-22/(-0,2x2√5);0) > B(10√2+10;0)
cette phrase n'a pas de sens : on compare des abscisses, ou des ordonnées, mais pas des points.
mais en effet, 55/√5 > 10√2 + 10
donc le point C est plus éloigné de l'hotel que le point B. oui
je ne suis toujours pas d'accord avec ta conclusion : "donc la webcam ne pourra pas assurer la surveillance du parking"
regarde le dessin : la tangente délimite au sol la zone qui sera surveillée... donc ...
je finis par avoir un doute avec cette webcam...
en fait, elle ne verra qu'après le point B (environ 45cm après), en bordure du parking.
mon idée était qu'elle peut voir si un malveillant tente de rentrer dans le parking,
mais évidement elle ne verra le parking lui même.
je vois ! en effet, ça fait sens. après il est vrai que la question se base sur la possibilité ou non de surveiller le parking : mais il est vrai que la tangente délimite la zone et pourrait voir un malveillant essayer d'entrer
dans tous les cas, merci beaucoup de m'avoir aidé  !! (et désolé de la longueur de la conversation, j'ai eu du mal)
!! (et désolé de la longueur de la conversation, j'ai eu du mal)