Inscription / Connexion Nouveau Sujet
Fonctions dérivées
Bonjour
Je sollicite votre aide pour une question sur laquelle je bloque dans un exercice. Je vais vous présenter toutes les questions de l'exercice et vous dire les réponses que j'ai trouvé au fur et à mesure jusqu'à la question sur laquelle je bloque.
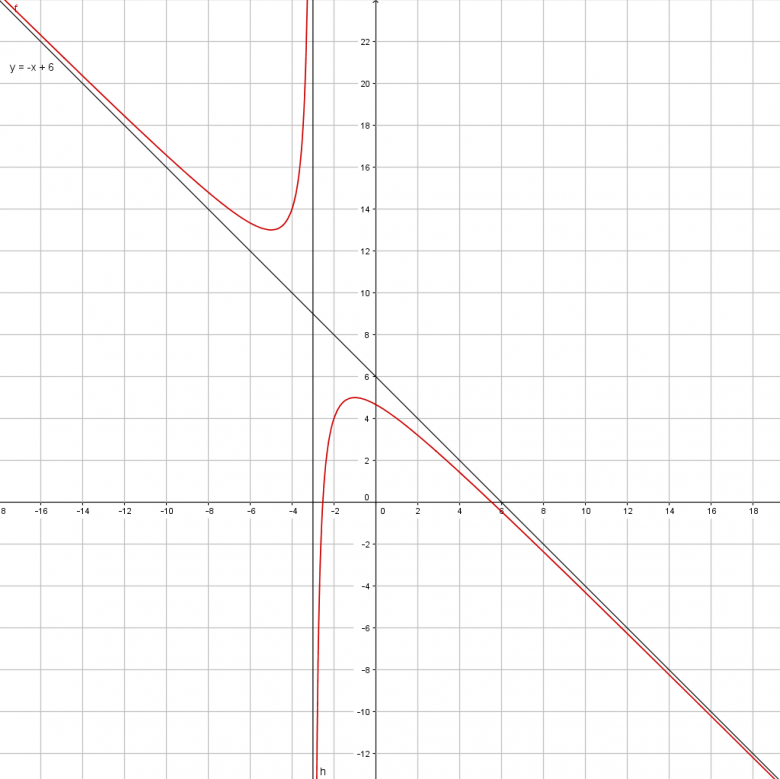
Soit f la fonction définie sur ]-infini;-3[U]-3;+infini[ par f(x)= -x²+3x+14/x+3.
On note (Cf) sa courbe représentative dans un repère.
1.a) Calculer f'(x) et vérifier que f'(x) = -x²-6x-5/(x+3)²
Donc ici j'ai fais le développement et j'ai trouvé ce qui est marqué aucun soucis.
1.b) Étudier le signe de f'(x) sur ]-infini;-3[U]-3;+infini[, puis dresser le tableau de variations de f sur ]-infini;-3[U]-3;+infini[.
Pour répondre ici j'ai calculé le delta de -x²-6x-5 et j'ai trouvé 2 solutions : -2 et -5.
Puis j'ai fais le tableau et j'en ai déduis qu'il y avait un maximum local en x2=-5 et un minimum local en x1=-2.
2. Étudier les positions relatives de la courbe (Cf) par rapport à la droite (D) d'équation y = -x+6.
Voici la question sur laquelle je bloque et j'hésite ici entre 3 manières de faire :
- soit je fais f(x)-(D) (j'ai fais celle-ci).
- soit f'(x)-(D).
- ou bien je calcule l'équation de la tangente de (Cf) puis je la soustrait à (D).
J'espère que vous pourrez m'aider,
Cordialement
Donc pour la question 2 la bonne manipulation ce serait f(x) - (D) donc -x²+3x+14/x+3-(-x+6) ?
J'ai recalculé le delta et en effet j'ai repéré une faute pour la solution -2, ce n'est pas -2 mais -1 c'est bien cela ? 
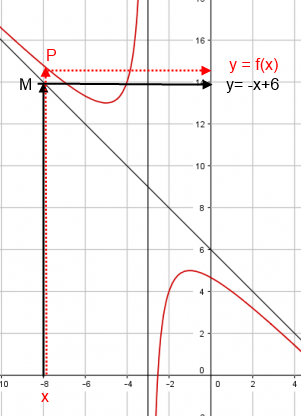
J'ai également à tracer (Cf) dans le graphique, ce que tu as gentiment fait ici. Seulement le souci c'est que je ne sais pas comment m'y prendre pour tracer précisément et sans faute la courbe, car j'allais la faire à main levée mais certaines mesures seront sans doutes fausses ainsi, comment pourrais-je faire? :/
ce serait d'étudier le SIGNE de f(x) - (D) (-x+6) donc -x²+3x+14/x+3-(-x+6) ?
N'as tu pas compris (voir mon premier message) l'IMPORTANCE des parenthèses dans l'écriture de f(x) ? C'est essentiel et OBLIGATOIRE quand on écrit une expression en ligne (sans trait de fraction) sinon gare aux erreurs quand tu rentreras des "fractions" sur ta calculatrice car elle, elle fait la distinction entre 5-3/2 (=3,5) et (5-3)/2 (=1).
Pour le tracé à la main, il faut faire un tableau de valeurs avec une bonne dizaine de points (tu as le droit de te servir du mode TABleau de ta calculatrice). Utilise du papier millimétré ou pour le moins des feuilles à "petits carreaux" (carrés de 5 mm)
Ah oui ! Je n'ai pas fais attention en le tapant ici mais sur la calculatrice je mets toujours les parenthèses dans ces cas là. Le calcul à faire pour la 2 est donc bien : (-x+3x+14)/(x+3)-(-x+6) ?
Le graphique est déjà présent sur ma feuille d'exercice où il y a déjà l'équation de (D) y = -x+6 de représenté seulement la plupart des points ne tombent pas juste sur le graphique je fais environ c'est ça ?
Le calcul à faire pour la 2 est donc bien : (-x+3x+14)/(x+3)-(-x+6)
Comme je te l'ai écrit en vert dans mon dernier message, il ne s'agit pas de "Calculer" mais d'étudier le signe de cette expression.
Le graphique ne te servira que pour VERIFIER que ce que tu trouveras par le calcul est compatible avec ce que tu vois sur la représentation graphique.
A toi de faire l'étude...
NB : pour étudier le signe d'un rapport (fraction) N(x)/D(x), on étudie le signe du numérateur puis celui du dénominateur et par un tableau de signes, on en déduit le signe du quotient.
Donc écrit l'expression dont tu dois étudier le signe sous la forme d'un quotient N(x)/D(x)
Étudier le signe c'est la question 1.b) moi je parlais de la question 2. qui est d'étudier les positions
Étudier le signe c'est la question 1.b) moi je parlais de la question 2. qui est d'étudier les positions
mais moi aussi je parle de la question 2

La courbe (Cf) est au dessus de la droite (D) si f(x) > -x+6
donc si f(x) - (-x+6) >0 donc si f(x) - (-x+6)est.... positif !
Ah d'accord, j'ai fais le calcul et voici les résultats :
Je rappelle le calcul : ((-x²+3x+14)/(x+3))-(-x+6)
Ligne suivante j'ai : ((-x²+3x+14)(x+3)+(x+6))/(x+3)
Et à la fin j'ai : (-x*cube* +24x+48)/(x+3)
Puis ensuite j'ai fais le delta de -x*cube* +24x+48 et j'ai obtenu 2 solutions :
x1 = (-24 - *racine de 768*)/(-2) et x2 = (-24 + *racine de 768*)/(-2)
Est-ce la bonne manipulation jusqu'ici avant que je ne détaille le tableau de signe et de variation par suite, que j'ai fais.
Ah d'accord, j'ai fais le calcul et voici les résultats :
Je rappelle le calcul : ((-x²+3x+14)/(x+3))-(-x+6)
Ligne suivante j'ai : ((-x²+3x+14)(x+3)+(x+6))/(x+3)
NON ta réduction au même dénominateur est fausse (1ère erreur)
Et à la fin j'ai : (-x*cube* +24x+48)/(x+3)
et ensuite tu appliques à un polynôme du TROISIEME degré, des formules et une démarche qui ne sont valables que pour le SECOND DEGRÉ
Puis ensuite j'ai fais le delta de -x*cube* +24x+48 et j'ai obtenu 2 solutions :
x1 = (-24 - *racine de 768*)/(-2) et x2 = (-24 + *racine de 768*)/(-2)
Est-ce la bonne manipulation jusqu'ici avant que je ne détaille le tableau de signe et de variation par suite, que j'ai fais.
J'ai rectifié l'erreur je pense :
f(x) - y = ((-x²+3x+14)/(x+3))-(-x+6)
= ((-x²+3x+14)-(-x+6)(x+3))/(x+3)
= (-x²+3x+14+x²+3x-6x-18)/(x+3)
= -4/(x+3)
C'est juste ainsi ?
Oui, c'est la bonne expression.
Il te faut maintenant étudier son signe pour comparer f(x) et ce que tu as appelé y (=-x+6), pour savoir si c'est Cf qui est au dessus de la droite ou... le contraire.
Comment je fais pour étudier son signe sans utiliser delta ?
Le signe du quotient
Tu planes avec ton delta
 (humour)
(humour)
Pour étudier le signe d'un quotient, on étudie :
1) le signe du numérateur (pas trop compliqué ici !)
2) le signe du dénominateur x+3
puis avec un tableau de signes on déduit le signe du quotient
J'ai essayé d'en faire un tableau de signe avec :
- une ligne pour x (j'y ai mis *-infini*, -3 et *+infini*)
- une ligne pour -4
- une ligne pour x+3
- une ligne pour f(x) - y
Seulement je ne sais pas comment le compléter, j'ai l'impression qu'il n'y a rien.
Les professeurs de maths que j'ai eu jusque maintenant m'ont souvent dit d'avoir le réflexe de sortir delta dès que j'entends ou vois "étudier le signe de ..." 
PS : Quelle blague haha 
Le numérateur -4 ne dépend pas de x ; quelle que soit la valeur de x, -4 est toujours... négatif (évident).
Le dénominateur (x+3) est un binôme du premier degré (forme ax+b) : bien avant (en 3ème et seconde) que tu n'entendes parler de "delta" (QUI NE SERT QUE POUR LES TRINOMES DU SECOND DEGRE ax²+bx+c), tu as du apprendre à trouver pour quelle(s) valeur(s) de x :
x+3 est NUL <==> x+3 = 0 <==> x = -3
x+3 est POSITIF <==> x+3 >0 <==> x >-3 donc x
x+3 est NEGATIF <==> x+3<0 <==> x <-3 donc x
D'où le tableau récapitulatif.....

Ah d'accord, merci pour le récapitulatif avant le tableau j'en avais besoin 
C'est ce que j'avais fais sinon pour le tableau hormis le fait que les 2 barres sous le "-3", vu que c'est la valeur interdite, je les avaient mises dès la première ligne du tableau (-4). Mais j'ai compris le raisonnement désormais.
J'ai juste une question quand à l'interprétation des résultats, est-ce que je pourrais placer les termes "maximum local" et "minimum local" ici ?
Pour le maximum et le minimum, cela n'a rien à faire ici.
Il doivent apparaître dans le tableau de variations de f (question 1b).
D'accord je les avaient mis pour la question 1.b).
J'aurais un juste une dernière question à vous poser, je pense que je ne comprends pas la consigne ici : "Montrer que la courbe (Cf) admet deux points E et F où la tangente est parallèle à la droite d'équation y = 3x."
Est-ce qu'il faut donc transformer f'(x) ici en équation de tangente ?
transformer f'(x) ici en équation de tangente
Je ne sais pas ce que tu entends par là....
mais fais le et on verra ce que tu obtiens.
Rappel de cours (important)
la tangente à la courbe Cf représentative de la fonction f au point A d'abscisse a est.... f'(a)
L'équation de la tangente à Cf en A(a ; f(a)) est : Y = f'(a) (x-a) + f(a).
J'ai pensé que cette équation pouvait être appliquée ici afin de trouver les deux points E et F où la tangente est parallèle à la droite d'équation y = 3x.
Pour que deux droites soient parallèles, il faut que leurs coefficients directeurs soient égaux (cours de 3ème).
La droite d'équation y = 3x a pour coefficient directeur, a = .....?
La tangente au point d'abscisse a a pour coefficient directeur.....
Si ces coefficients directeurs sont égaux, on a ........
équation dont l(inconnue est a.
En résolvant cette équation, on obtient les valeurs de a, abscisse(s) du ou des points de Cf où la tangente est parallèle à la droite d'équation y = 3x.
La droite d'équation y = 3x a pour coefficient direction a = 3 ?
La tangente au point d'abscisse a a pour coefficient directeur f'(a) ?
Si ces coefficients directeurs sont égaux, on a f'(a) = a ?
La droite d'équation y = 3x a pour coefficient directeur m = 3 ? oui mais ce n'était pas très judicieux de ma part d'appeler ce coef directeur "a" puisqu'à la ligne suivante j'utilisais la même lettre pour quelque chose de différent
La tangente au point d'abscisse a a pour coefficient directeur f'(a) ?
OUI
Si ces coefficients directeurs sont égaux, on a f'(a) = m avec m=3 ?
Donc il te faut résoudre l'équation
f'(a) = 3
D'accord j'ai compris l'enchainement.
Pour résoudre f'(a)=3 je ne vois pas comment m'y prendre, mais j'ai observé graphiquement que la droite d'équation y = 3x au point d'abscisse 3 correspond une ordonnée de 7. Et étant donné que la tangente doit être parallèle à cette droite, je pense qu'il s'agit d'un des points E ou F ?

Tu as calculé dans une question précédente f'(x) donc pour avoir f '(a) il suffit de remplacer dans l'expression de f'(x), la variable x par... a !
Tu écris que f '(a) = 3 et tu résous cette équation où l'inconnue est a.
Donc ça donne :
f'(3) = (-3² - 6*3 - 5)/(3+3)² = (-9 -18 +5)/36 = -32/36 = -8/9 ?
Non tu fais n'importe quoi. Tu es censée chercher "a" et tu prends a= 3 !!! Si a=3, il n'y a plus rien à chercher

f '(x) = (-x²-6x-5) / (x+3)²
donc
f '(a) = (-a²-6a-5) / (a+3)²
On cherche la (ou les) valeur(s) de "a", telles que :
f'(a) = 3
(-a²-6a-5) / (a+3)² = 3
Tu n'as plus qu'à résoudre cette équation dans laquelle l'inconnue est a.
Lis d'abord le message qui précède.
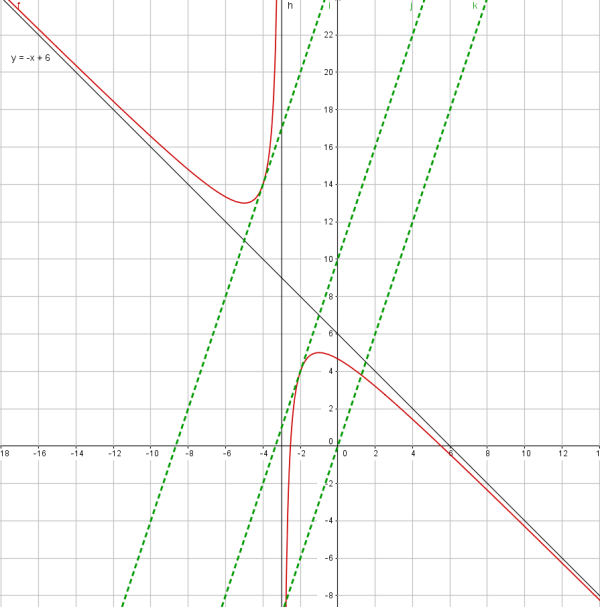
.... et à trouver une réponse compatible avec la figure ci dessous 
Voilà ce que je trouve en effectuant le calcul :
(-a² - 6a - 5)/(a+3)² = 3
(-a²-6a)/a²+6a = -1 (j'ai remarqué ici que l'équation de f'(a) s'annulait : -a² avec a² et -6a avec 6a)
f'(a) = -1
Voilà ce que je trouve en effectuant le calcul :
(-a² - 6a - 5)/(a+3)² = 3
(-a²-6a)/a²+6a = -1
d'où sors tu cette chose ? comment as tu simplifié ????
(j'ai remarqué ici que l'équation de f'(a) s'annulait : -a² avec a² et -6a avec 6a)
incompréhensible
f'(a) = -1
Je croyais que f'(a) devait être égal à.......3
et où est TA réponse ??
J'ai résolu l'équation de départ pourtant :
f'(a) = 3
(-a - 6a - 5)/(a+3)² = 3
(-a² - 6a)/(a²+6a+9)=8
(-a²-6a)/(a²+6a) = 8- 9 = -1
f'(a) = -1
Je ne comprends pas du tout comment tu as conduit ce calcul... faux . Quelles règles de 4ème et 3ème, as tu appliquées ?
f'(a) = 3
(-a² - 6a - 5)/(a+3)² = 3
On peut multiplier chaque membre d'une égalité par un même nombre non nul, on obtient une nouvelle égalité.
Je multiplie chaque membre par (a+3)² si a -3
-3
-a² - 6a - 5 = 3 (a+3)²
Ceci est une équation du second degré par rapport à "a".
Il suffit de l'écrire sous la forme "trinome du second degré en a"=0 et de la résoudre....
Ah d'accord. Donc la suite ce serait :
-a²-6a-5=3a²+18a+27
-4a²-24a-32=0
Delta = b²-4ac = (-24)²-4*(-4)*(-32) = 64 = 8²
Delta > 0 : 2 solutions réelles distinctes :
x1 = (-b- delta)/2a = (24-8)/(-8) = -2
delta)/2a = (24-8)/(-8) = -2
x2 = -4
S={-2;-4} ?
Oui pour les valeurs trouvées...
...mais il serait fort utile que tu répondes par une phrase rédigée à la question posée (relis l'énoncé). Cela redonnerait du sens à ton calcul et peut être pourrais tu ainsi aller VOIR (histoire de VERIFIER ta réponse) sur la dernière figure que je t'ai envoyée que l'on peut y LIRE ces fameuses valeurs -2 et -4....

Ah oui les résultats sont visibles sur le graphique en effet. En phrase de réponse est-ce que ça convient :
La courbe (Cf) admet donc 2 points E et F de coordonnées respectives [-4;14] et [-2;14] où la tangente est parallèle à la droite d'équation y=3x. ?
Après juste un petit soucis, je n'arrive pas à trouver le calcul qui permette de justifier les ordonnées des points car je les ai déterminés en observant le graphique ici mais il faut un calcul. J'ai essayé de remplacé x dans f'(x) par -4 je n'ai pas obtenu 14, de même pour -2.
E et F de coordonnées respectives [-4;14] et [-2;14]
Étourderie de lecture ou de recopie ?
justifier les ordonnées des points
Là c'est plus grave !!
Les points E et F appartiennent à la courbe Cf représentative de f donc comme pour tous les points de cette courbe [dont l'équation est y =f(x)], si leur abscisse est x, alors leur ordonnées est..... f(x) tout simplement.
Erreur de frappe je voulais dire [-2;4] ^^'
Le problème est que lorsque je remplace x dans l'équation de f(x) par -4 ou par -2 je n'obtiens pas ces ordonnées :
f(-4) = (4²+3*(-4)+14)/(-4+3) = -18 ( 14)
14)
f(-2) = (2²+3*(-2)+14)/(-2+3) = 12 ( 4)
4)
bien sûr que... NON.
-x² = -[(-4)²] = -[(-4)*(-4)] = -[+16] =-16
Tu as de grosses lacunes sur des connaissances... de BASE 
Fais très attention à développer pas à aps tes calculs..... comme ci dessus !
Au passage :
-x² n'est pas égal à (-x)² = (-x)*(-x) = x²
-x² c'est -(x²)
D'accord et bien c'est ce que j'avais fais dans le calcul tout à l'heure lorsque j'ai trouvé une ordonnée de -18 pour -4, j'avais fais 4² et non -4² car je m'étais dis qu'il y avait changement de signe justement.
Donc si j'ai compris il faut faire :
f(-4) = (-(4²) + 3*(-4) + 14)/(-4+3) = 14 ah oui voilà c'est ça
f(-2) = (-(2²) + 3*(-2) + 14)/(-2+3) = 4
D'accord et bien c'est ce que j'avais fais dans le calcul tout à l'heure lorsque j'ai trouvé une ordonnée de -18 pour -4, j'avais fais 4² et non -4² car je m'étais dis qu'il y avait changement de signe justement.
Je ne sais pas si, pour toi, cette phrase a un sens mais moi je ne la comprends pas

Ma seule certitude est que ta réponse -18 était fausse...
N'as tu pas une calculatrice avec un mode TABleau pour pouvoir VERIFIER tes calculs qui, quoi que tu en dises, sont assez... hasardeux.
C'est moi qui ai écrit la phrase donc forcément je la comprends, mais c'est vrai que pour une autre personne elle peut ne pas être claire ^^'
En tout cas ce que je voulais dire c'est que j'avais fais une erreur en calculant lorsque j'avais obtenu -18. Mais désormais j'ai trouvé l'erreur et j'ai refait le calcul correctement cette fois et ça m'a bien donné une ordonnée de 14 pour -4, et une ordonnée de 4 pour -2.
Oui j'ai vérifié les résultats avec ma calculatrice et ils sont justes.