=

=


=

Oh non j'avais bien mi


sur ma copie

Oups

Othnielnzue23 @ 05-12-2019 à 21:08

Oh non j'avais bien mi


sur ma copie

j'ai bien aimé quand tu as dit qu'il n'y avait rien sur le site pour toi car tu maîtrisais tout ce qu'il y avait
eh beh....
c'est enfin juste

vu ton faible le niveau de maitrise de tels calculs, faut pas sauter des étapes en les faisant de tête à la va comme je te pousse ...

    oui

    oui

là ensuite tu rates des trucs importants en les faisant de tête et donc en te plantant.

    faux
les étapes omises sont explicitement (tu dois les écrire explicitement sur papier vu que te te plantes aussi régulièrement !!!)





    (tu as eu du mal à additionner correctement ces deux fractions avec tes 7/9 et autres erreurs du genre)

et le plantage vient là : développer le facteur ( -3)

développement d'une somme

et moins trois multiplié par moins 4 neuvièmes ça fait :
• règle des signes
• comment multiplier une fraction par un nombre
• maitrise de ça c'est du niveau collège

et ça ne fait pas -4/9
...

enfin ...

salut

une méthode pour ne pas s'em.... avec des fractions ... ou en tout cas bien moins de fractions :

Voir 21 h09 ...

je sais, mais au bout de combien d'échanges de calculs faux ?

oui, j'ai vu tes messages parus pendant que je tapais tout ça
c'est pour ça que je dis "enfin"
tout ça parce que tu n'aurais simplement pas recopié ici correctement le résultat écrit sur ta feuille pfff ... et on se demande même si ce n'est pas du bourrage de mou que c'était prétendument correct, alors que ta courbe de g était chaque fois fausse)

carpediem
la forme factorisée ne sert absolument à rien dans cet exo "en (de celle de f) déduire la courbe de g"
c'est la forme canonique qu'on veut.
pour appliquer la translation transformant l'une en l'autre sans aucun nouveau calcul de points.

J'avais bien trouvé sur ma copie bien avant tout çà , seulement que j'ai saisit 4/9 au lieu de  4/3 .

Oui puis que j'utilisais la mauvais forme canonique.

Bon ... Voici ce que j'obtiens enfin.

Bonne forme canonique , bonne courbe .

On attaque la 2e question .

et

la courbe de g doit être exactement la translatée de la courbe de f (au papier calque en quelque sorte)
pas un patatoïde qui y ressemble aussi peu que tu le fais, un minimum de soin tout de même est nécessaire !!!
et 4/3 ne fait par 1,5 ni 1/3 ne fait 0,5
bref, dessin de cochon.

passons
il faut espérer pour toi que tu retraceras tout ça bien plus proprement au propre !

autre façon de voir :
dire que la courbe déja tracée de f est  la courbe de g (sans rien retracer du tout) mais dans un autre repère :



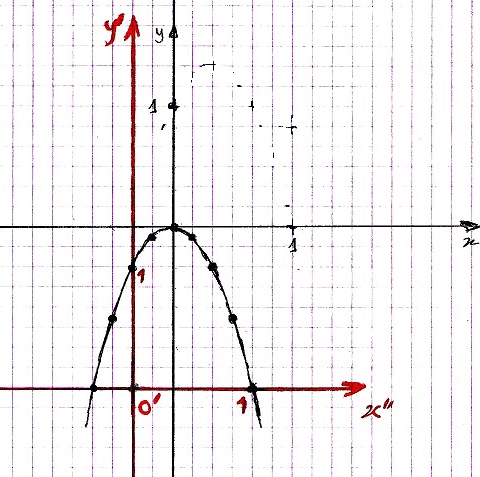
la courbe tracée est la courbe de f dans le repère noir xOy
et la même courbe est la courbe de g dans le repère rouge x'O'y'

2ème question
f(x) : même méthode, calculer un certain nombre de points et les relier, en accord avec l'allure de la fonction inverse dans le cours.

pour g(x) il faut l'écrire sous la forme équivalente g(x) = b + f(x-a)
pour faire apparaitre le vecteur de translation transformant la courbe de f en courbe de g
c'est à dire écrire g(x) sous la forme
en effectuant à l'envers les étapes qui transformeraient cette forme en
(mise au même dénominateur etc)
ou en effectuant effectivement ces étapes avec a et b écrits a et b, puis en identifiant les coefficients.

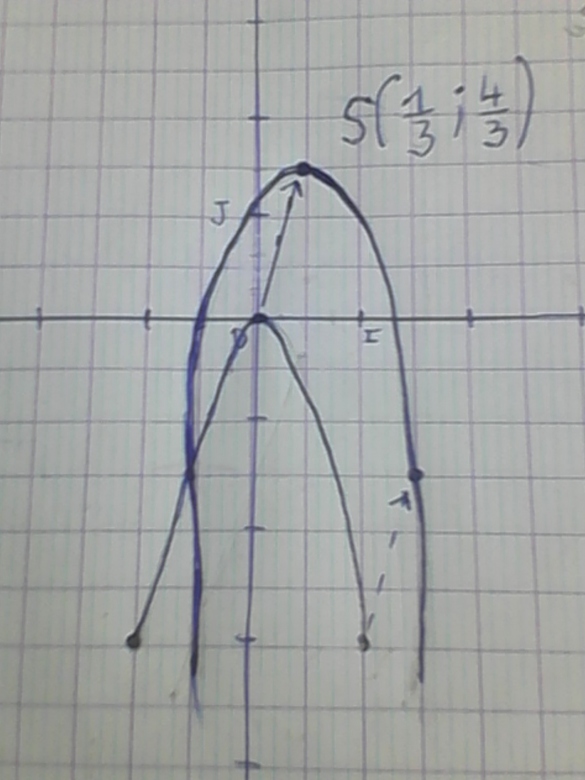
Dit autrement :  On a un point (1/3, 4/3) ;
4 pommes, c'est 4 fois plus qu'une pomme, et de la même façon, 4/3, c'est 4 fois plus grand que 1/3

Or sur le dessin, le seul truc qu'on voit bien, c'est que la hauteur de la fléche, c'est 3 fois plus que la base.  Donc c'est faux.

OK monsieur .

et choisir pour unité 2 carreaux quand on travaille avec des 1/3 ....et cela lui avait pourtant été soufflé....

Bonsoir .


Veuillez m'excuser pour mon abscence durant  ces deux jours .