J'ai d'abord trouvé l'ensemble de définie des fonctions .

* l'ensemble de définition

1) Df=lR .

2) Df=lR\{0}

3) Df=lR\{1/2}

4) Df=[2;+oo[

réécris avec les "bons n°

Quels numéros ?

Bonjour,

ne pas confondre la fonction f et la fonction g
ni les numéros des questions ...
donc tes réponses à "3" et "4" (sic !!) sont fausses

déja parce que ce n'est pas les questions 3 et 4
et ensuite ce n'est pas la fonction f
et enfin la vraie question 4 n'est pas traitée du tout.

Ah oui

1) Df=lR

2) Df=lR\{0}

3) Df=[0;+oo[

4) Df= [0;+oo[

Salut monsieur mathafou

Oui, là c'est bon

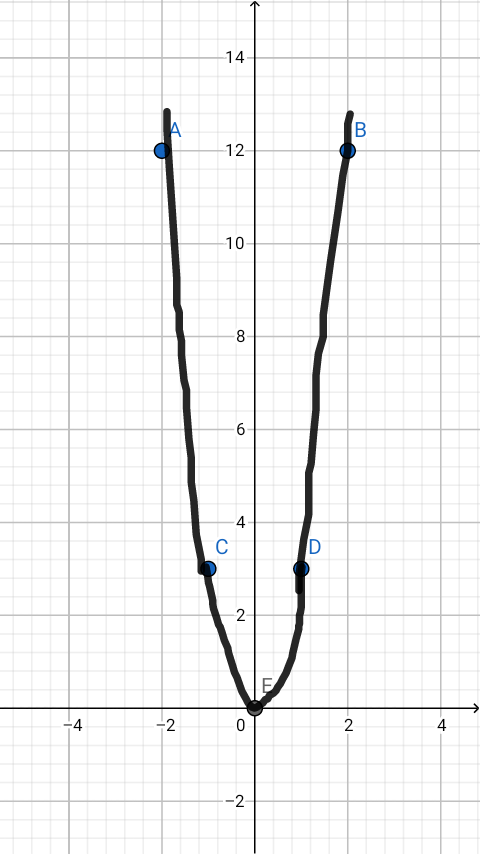
il te reste surtout à tracer les courbes demandées "sans calculette ni logiciel" des fonctions f
ça se fait en calculant (à la main "sans calculette" !!) quelques points bien choisis, en les reportant sur du papier quadrillé et en les reliant par des "courbes harmonieuses" à main levée.

pour les fonctions g "en déduire" ça se fera sans aucun calcul supplémentaire de points
c'est le but de l'exercice, de considérer les relations géométriques entre les courbes de f et de g : translations, symétries etc

OK monsieur .

Merci à vous monsieur mais comment choisir ces points là ?

1 et 2 sont connues en seconde !!

Oui , j'ai des questions .

Dans un plan muni d'un repère (O;IJ) , la représentation graphique de la fonction f est l'ensemble des points M de coordonnées (x;y) tel que :

- l'abscisse x Df

-l'image de x par f est f(x)=y

1) on a Df=lR  (xDf ) si prenons x=5 , çà marche ?

Fonctions : Généralités
Présentation des fonctions carré et inverse
Fonction polynôme de degré 2 et parabole

Merci infiniment .

je reviens sur
"comment choisir ces points là ?"

de façon à ce que les points soient dans la feuille sur laquelle on va tracer la figure, selon l'unité choisie
qu'ils soient suffisamment rapprochés et nombreux pour que le tracé à main levée ne soit pas trop aberrant, mais pas trop pour ne pas se fatiguer inutilement à en calculer plus que de raison
choisis dans un intervalle [a; b] qui va montrer les parties intéressantes de la courbe

bref c'est à toi de les choisir
presque n'importe lesquels, juste selon les critères subjectifs ci dessus.

par exemple pour tracer f(x) =3x²
compte tenu du cours qui dit quelle est la forme générale de cette courbe
déja on n'en calcule que la moitié, vu l'axe de symétrie
le sommet est tout calculé, ça en fait déja un
deux ou trois autres dans [0; +oo[ (à cause de la symétrie) que l'on va choisir en fonction de l'échelle adoptée (choix de l'unité du repère) et pour que les calculs soient simples (pas de calculette est-il dit)
compte tenu du coefficient 3 de 3x², on peut imaginer prendre une unité du repère = 3 cm par exemple, c'est un choix parfaitement subjectif et personnel, on peut choisir 6cm si on veut "zoomer" d'avantage sur l'origine.
x = 1/3 donne alors un nombre entier de cm aussi bien en abscisses que en ordonnées
donc un point facile à calculer et à tracer
etc (à toi d'en choisir d'autres dans le même genre)

D'accord monsieur .

Alors j'ai choisit l'intervalle [-2;2] , mon tableau de valeur.

si tu veux
c'est un peu juste comme nombre de valeurs (seulement deux points de chaque côté) et tu en as oublié une absolument nécessaire

Et voici ce que j'obtiens pour la courbe .

Maintenant que j'ai construit (Cf) , comment en déduire la courbe de g (Cg) ?

avec une des fiches que je t'ai ciblées hier....

pas vu l'erreur
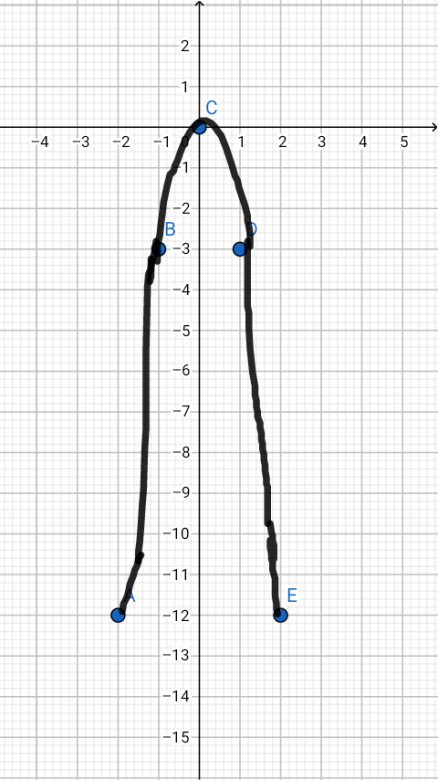
y = moins 3x^2
tes valeurs sont donc fausses et ton dessin aussi


les valeurs de y très élevées sont "peu intéressantes"
c'était le sens de ma suggestion de choisir une unité plus grande et de faire ainsi un "zoom" au voisinage du sommet, là où la courbure est la plus prononcée

pour construire Cg il faut comprendre la signification géométrique de quelle transformation purement géométrique (translation, symétrie, rotation, homothétie etc) transforme y=f(x) en y=g(x)
de façon la plus générale :
comment déduire la courbe de y = f(x-a) + b de celle de y=f(x)
quelle transformation géométrique transforme une courbe en l'autre.
ou ce qui revient au même : quel changement de repère fait afficher g(x) exactement sur la courbe de f(x) déja tracée dans le repère initial

et on applique ça en écrivant g(x) sous sa forme canonique

Merci à vous monsieurmathafou

Bonsoir , voici ce que j'obtiens .

comment déduire la courbe de y = f(x-a) + b de celle de y=f(x)
quelle transformation géométrique transforme une courbe en l'autre. : dans ce cas (Cg) s'obtient par translation du vecteur a +b .

Donc (Cg)=t a+b(Cf) .

une fiche qui peut t'intéresser Exemples de fonction inverse

Donc pour trouver a et b je fais la forme canonique de et je trouve :



Du coup j'ai mon a= et b=

C'est bon ?

c'est bien mieux
mais avec cette échelle là on ne verra pas grand chose pour mettre f et g sur le même dessin ...

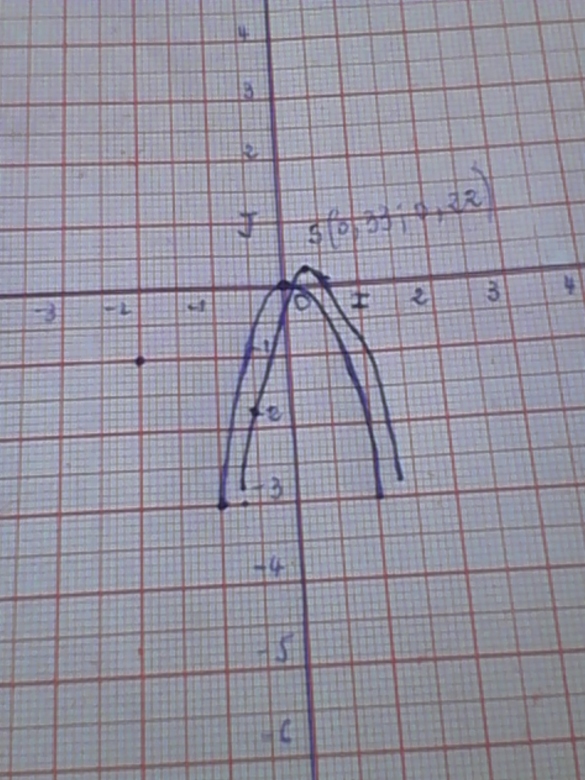
ma figure :
faite réellement sur papier sans tricher avec un placement des points sur géogébra interdit
ni un gribouillis fait avec le stylo de Geogebra et la souris :
vraiment pas pratique de dessiner quoi que ce soit à la souris à main levée, ou avec ses gros doigts sur un écran tactile c'est pareil
on fait tout de même bien mieux avec un vrai stylo sur une vraie feuille de papier !!
surtout que c'est respecter les consignes de l'énoncé de ne pas utiliser du tout d'écran de quoi que ce soit.



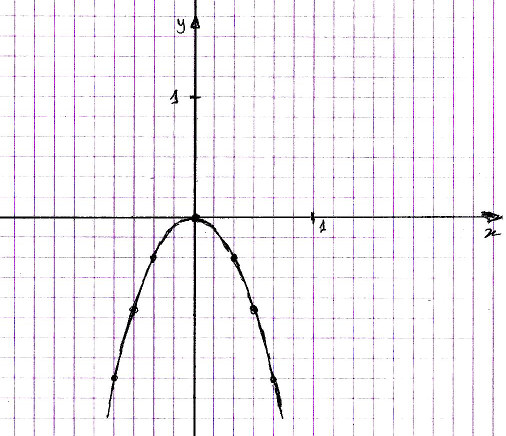
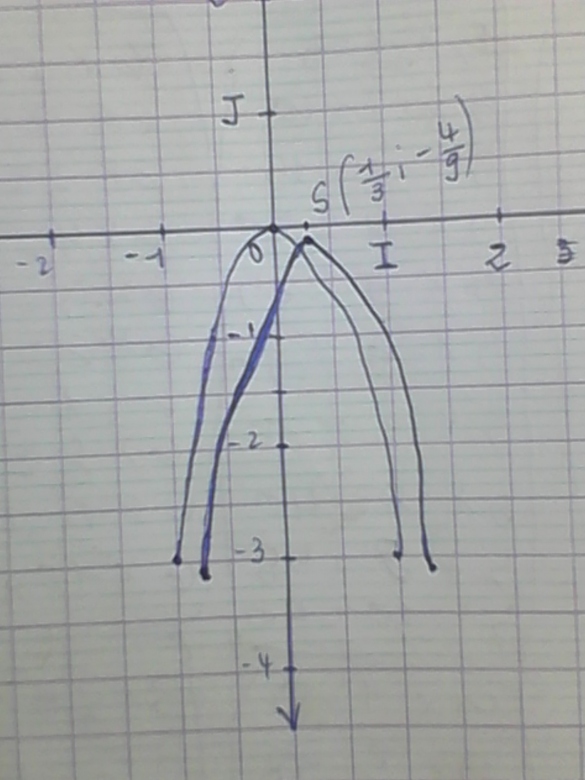
et avec 3 points de chaque côté, plus le sommet, c'est tout de même plus précis que avec deux seulement (déja dit, et il n'y a pas que les nombres entiers dans la vie !!)
j'aurais même pu rajouter le point (1/6; -1/12) et son symétrique pour plus de précision au voisinage du sommet ..

Ah d'accord monsieur .

la forme canonique c'est pas         c'est    
pour lire directement dessus les coordonnées du sommet et donc les coordonnées du vecteur de la translation.
et donc reporter les points sans calcul directement à l'aide du quadrillage si on a pris la précaution comme moi de choisir une unité qui est un multiple de 3 carreaux de la grille

ou à l'inverse de décaler le repère du vecteur opposé pour qu'il n'y ait rien de nouveau à tracer du tout.

OK monsieur .

Voici ce que j'obtiens pour la première question .

ta forme canonique est fausse.
donc ton sommet aussi.

Ah oui je devais trouver

Oups

Othnielnzue23 @ 05-12-2019 à 19:03

Ah oui je devais trouver

toujours faux, redéveloppe, et tu verras bien que c'est faux.
le terme constant serait   -3/9 -4/9 = -7/9 ≠ 1

Et donc je devais obtenir ceci .

J'ai repris et je trouve même chose .

développe et vois si tu trouves comme l'énoncé

Il y'a donc une erreur , mais où ?

Je crois que je vais utiliser ∆ et ensuite factoriser avec les zéros trouvés.

illisible.

je suppose : la multiplication finale par -3 mal effectuée
erreur de multiplication d'une fraction par un nombre
et erreur de signe

factoriser ne sert absolument à rien du tout pour trouver le vecteur de la translation.
et le problème n'est pas la méthode mais les erreurs de calculs
(mauvaise maitrise des développements de collège)

et si tu fais le même genre d'erreurs avec ta factorisation tu seras bien avancé avec un truc inutile et en plus faux, tiens...

c'est uniquement savoir développer correctement et rien d'autre.

Je trouve enfin .