Bien  Je reprends


Avez-vous résolu l'équation en ?

j'ai trouver que pour que f'(-2) = 0 m doit faire -8

mince cest m= -6 pour que f'(-2) = 0

bien on sait donc  que si    les dérivées de et de sont nulles

Il est donc possible que pour cette valeur de soit   les fonctions et admettent un extremum en

si , admet -elle un maximum en

En est-il de même pour ?

Non c'est bien -8

non c'est bien m = -6 c'est ma faute j'ai mal dit la dérivé de f
donc la fonction de f c'est x³ -3/2*x² + 3mx
et la dérivé c'est 3x²-3x+3

Bon cela ne change pas fondamentalement

Quel est le sens de variation de   ? de ?

Ou plus simplement quel est le signe de ?

le signe de f'(x) est de

mince

le signe de f'(x) est de - 0 +

mais est ce que je dois calculer f(-6) ou f(-2)

Non vous avez un trinôme du second degré  
il est du signe de a sauf pour les valeurs comprises entre les racines

On a déjà quelle est l'autre racine   ?

l'autre racine est -6

Peu nous chaut la valeur du maximum.

On veut le signe de

comme le signe de a est positif donc le signe est - 0 + non ?

Non    on sait maintenant que puisque c'est la seule possibilité  pour que les deux fonctions  aient un maximum au même point

ah bah oui on calcule delta ce qui fait

x1 = 3
x2 = -2

bien
quoique l'usage du   est un peu lourd

donc maintenant quel est le signe de   le sens de variation de Quelle conclusion quant à l'extremum en

le signe de de f'(x) est + 0 - 0+ est je n'ai pas compris votre dernier question

Bien     la fonction est donc croissante  décroissante croissante

Qu'a-t-on en ?  

j'ai f(-2) = 22

Aucun intérêt

Quelle est la nature de l'extremum ?

comment sa la nature ? qu'entendez vous par la ?

Deux possibilités soit un maximum soit un minimum

il ya un maximun qui est de 22 es un minimun qui est de -40.5

Il n'y a qu'un extremum local qui nous importe celui en

En f admet bien un maximum   En est-il de même pour ?

oui pour g aussi il admet un maximun en -2

il faut le prouver,  pour l'instant on sait qu'il y a un extremum  
Quel est le sens de variation de ?

les signe sont de + 0 - donc croisante et décroissante

Oui ou alors  en utilisant le signe du coefficient de   comme vous l'avez-vu en seconde

Pour m=-6 les deux fonctions ont un maximum local en

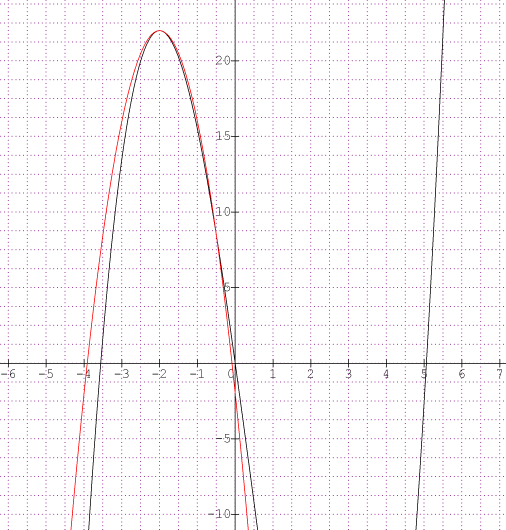
oui mais maintenant qu'on sait que les deux fonction on un maximun pour abscisse -6 on a pas l'ordonnée comment fait on pour calculer des coordonés ?

Non
La valeur de est l'abscisse est   et vous avez  calculé l'ordonnée 22

donc l'abssice du point est -6 et ordonés 22 ?

Non il faudrait faire attention

je viens de vous écrire que pour les deux fonctions admettent un maximum égal à 22 obtenu pour

Sur ce, j'arrête  maintenant.   Je reviendrai dans quelques heures

Merci Beaucoup je crois que c'est bon, je viens de terminer l'exercice car, j'ai trouver la valeur de m est ses coordoné

Merci a tout ceux qui m'ont aidé

De rien

pas de quoi