Inscription / Connexion Nouveau Sujet
Fractions & problemes
Salut voilà j'ai un exercice j'aimerai qu'on me corrige le 1) et pour le 2) je n'ai pas compris j'aimerai qu'on me guide
Exercice :
1°)Factorise les expresseions suivantes :
E = (x + 7)² - 36
F = 4x²+ 8x + 4
G = (x + 13) (x+1) - 4 (x+1)²
F = 4x²+8x+4
F = (2x + 2)²
G = (x + 13) (x+1) - 4 (x+1)²
G = (x +13) (x+1) - 4 (x+1) (x+1)
G = (x+1) [(x+1) -4 (x+1) (x+1)]
G = (x+1) [(x+1) +4 -x -x +x+1]
G = (x+1) [x+1 +4 - x - x +x +1]
G = (x+1) 6
pour la E j'ai pas réussi commment y faire
2°)
Dans cette question, x désigne un nombre positif.
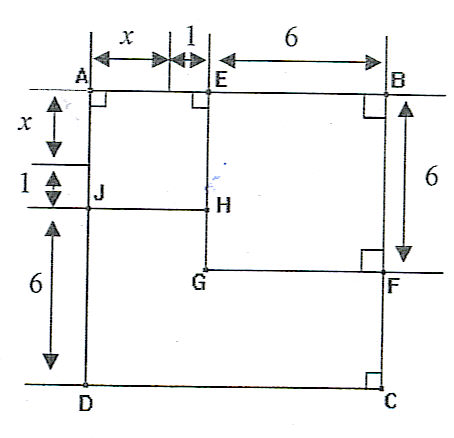
Après avoir observé la figure ci contre.
a) Exprime en fonction de x l'aire A du polygone AEGFCD.
b) Pour quelle valeur de x l'aire A est elle égal à quatre fois l'aire du carré AEHJ
voilà merci de m'aidé
Salut,
Pour la E = (x + 7)² - 36 :
Tu doit reconnaitre une identité remarquable car 36 = 6²
donc:
(x + 7)² - 36 = (x + 7)² - 6²
= (x+7-6)(x+7+6)
= (x+1) (x+13)
Voila pour la F elle est bonne mais la G un petit problème:
G = (x + 13) (x+1) - 4 (x+1)²
G = (x +13) (x+1) - 4 (x+1) (x+1)
G = (x+1) [ (x+13)- 4(x+1) ]
G = (x+1) (x+13-4x-4)
G = (x+1) (-3x+9)
Voila 
1°) E est du type A² - B² donc tu factorises en utilisant l'indentité remarquable a² - b² = (a + b)(a - b)
E = (x + 7 - 6)(x + 7 + 6) = (x + 1)(x + 13)
F est juste mais G est fausse:
G = (x + 1) [ (x + 13) - 4(x+1)] = (x + 1) (x + 13 - 4x - 4)= (x+1)(-3x+9) = 3 ( x + 1)(3-x)
2°) L'aire de AEGFCD est l'aire de ABCD moins l'aire de EBfg d'où:
Aire de AEGFCD = (1+x+6)² - 36 = (x+7)² - 36 et c'est E
L'aire de AEHJ vaut (1+x)² d'ou il faut résoudre:
(x+1)(x+13)=4(1+x)² si x=1 c'est ok sinon tu simplifies par x+1 d'ou:
x+13 = 4+4x
3x = 9
x = 3


