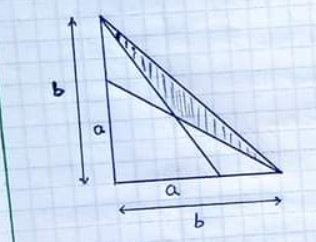
Imad67, on te l'a déjà dit...
Quel est l'énoncé ? que trouves-tu ?
détaille ce que toi tu as trouvé si tu veux qu'on regarde !!

Bonjour,

J'ai cherché une solution géométrique à base de Thalès, pas trouvé, et par dépit j'ai tenté une solution analytique en introduisant un repère évident, puis en calculant les coordonnées du sommet obtus du triangle, du milieu du côté opposé, la longueur de la hauteur correspondante, la longueur de la base correspondante, et finalement la surface, et j'arrive à :



L'équation aux dimensions est correcte, les valeurs extrêmes de S :
a = 0 S = b²/2
a = b S = 0
sont bonnes, au-delà je ne sais pas si c'est exact

Et surtout, je serais preneur d'une solution géométrique

Bonjour,
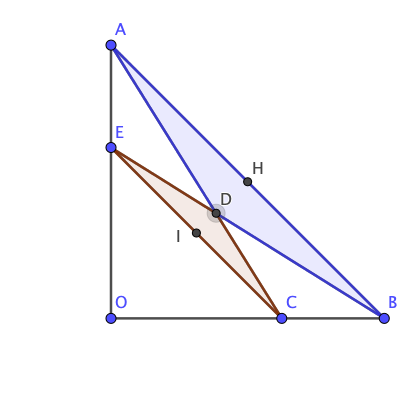
Sans repère
aire du trapèze =aire  du triangle AOB-aire du triangle EOC=(b^2-a^2)/2
aire de trapèze = (B+b)*h/2  
on en déduit IH  √2(b-a)/2
on  montre
aire du triangle DAB-aire  du triangle DEC=(b-a)^2/2
ce qui permet de déterminer DH
puis l'aire du triangle ADH

Bonjour PLSVU,

Très élégant, peux-tu aller jusqu'au bout de ton raisonnement, histoire de voir si nous obtenons bien la même chose ?

Pour DH, en reprenant tes notations, j'avais trouvé :

Bonjour,
@LeHibou,
Je trouve comme toi pour DH.
J'ai utilisé la proportionnalité des dimensions des triangles ADB et EDC qui donne ID = (a/b) DH.
Mais en 3ème...

@PLSVU,
Pour calculer IH, il me semble que l'on peut faire
OH - OI = b 2/2 - a2/2.

Bonjour  à vous deux,
OK
puis l'aire du triangle ADB

  aire du triangle ADB=(b√2)*DH/2=b^2(b-a)/2(b+a)

coucou

Merci malou