Inscription / Connexion Nouveau Sujet
géométrie optimisation
Bonjour,
Pour relier sa maison à sa bergerie monsieur Martin doit construrie un pont perpendiculaire au lit de la rivière qui traverse sa prairie. Il souhaite implanter le pont de façon à ce que le trajet de la maison à la bergerie soit minimal.
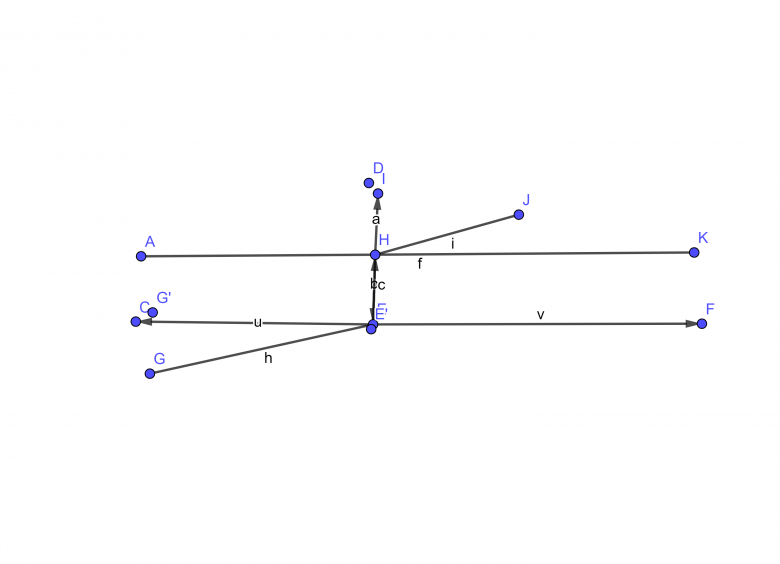
La maison de monsieur Martin est représentée par la point G, sa bergerie par le point J et les bords de la rivière, supposés parallèles par les objets AK et CF. Le pont est modélisé par le segment EH.
1) A l'aide d'un logiciel, réaliser la figure, puis conjecturer la position du segement [EH] rendant minimal le trajet de la maison à la bergerie.
2) Constriure le point G' image de G par translation de E qui transforme E en H
3) En déduire la construction des points E et H tels que le trajet de la maison à la bergerie soit minimal.
J'ai fait le schéma , je ne vois pas comment conjecturer la position de E et H.
D'après la propriété de la projection d'un point orthogonal M sur une droite
est le point de la droite
le plus proche du point M
Je pense que GEH devrait être alignés sur une droite perpendiculaire à AK et CF.
Je commence à utiliser Geogebra : le schéma n'est pas très bon.
Merci.
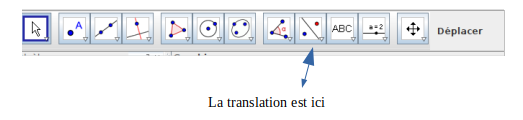
Bonjour
Il ne faut pas laisser le logiciel marquer tous les objets,
Tracez [G'J ] La droite (G'J) coupe (AK) en H
Bonjour
bon, c'est un début avec geogebra, mais tu vas devoir apprendre à utiliser vraiment les fonctionnalités du logiciel
car j'ai l'impression que tu as fait ça un peu au jugé
as-tu utilisé "tracer une droite // " du logiciel ?
as-tu utilisé "tracer une droite perpendiculaire" du logiciel ?
je ne crois pas
ensuite repasse régulièrement par la flèche tout en haut à gauche, pour ne pas créer des points partout ainsi dans ton dessin
et quand tu en crées qui n'ont pas lieu d'être, tu fais un clique droit sur le point que tu veux effacer, et tu le fais disparaître
OK ?
voilà à quoi tu dois arriver comme style de construction, avant toute autre chose
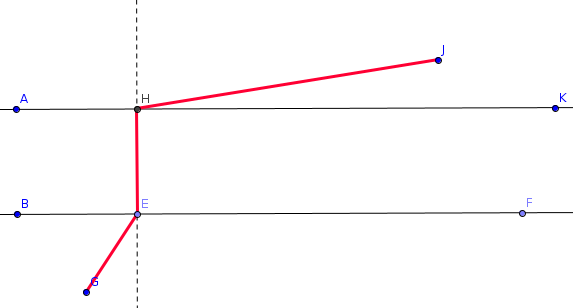
je laisse la main à hekla
Vous avez défini
Pour avoir l'image de G par cette translation écrire G'=G+w
Vous avez changé le nom des points ?
Oui, j'ai nettoyé le schéma et les lettres ont changé en même temps.
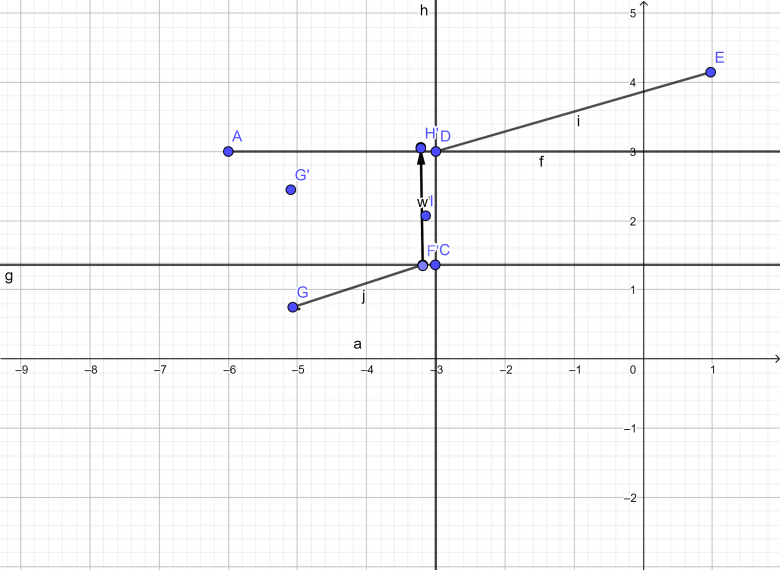
Voici les nouvelles lettres.
J'ai réussi à faire apparaître l'image G' de G.
La maison de monsieur Martin est représentée par le point G, sa bergerie par le point E et les bords de la rivière, supposés parallèles par les objets AB et g. Le pont est modélisé par le segment FH.
1) A l'aide d'un logiciel, réaliser la figure, puis conjecturer la position du segement [FH] rendant minimal le trajet de la maison à la bergerie.
2) Constriure le point G' image de G par translation de F qui transforme F en H
3) En déduire la construction des points F et H tels que le trajet de la maison à la bergerie soit minimal.
J'ai fait le schéma , je ne vois pas comment conjecturer la position de F et H.
D'après la propriété de la projection d'un point orthogonal M sur une droite \Lambda
est le point de la droite \Lambda
le plus proche du point M
Je pense que GFH devrait être alignés sur une droite perpendiculaire à AK et CF
Bonjour
et histoire de rajouter mon grain de sel :
encore faut il avant ça que les points F et H soient définis correctement et pas des points libres totalement indépendants du reste de la figure, placés "au pif" à peu près où on voudrait qu'ils soient
F et H sont les points D et C qui auraient dû être simplement renommés en F et H (dit l'énoncé)
et pas d'autres points créés indépendamment !
J'ai mis les points pour créer un vecteur
en parallèle de la perpendiculaire pour pouvoir créer l'image de G'de G.
pour vérifier que les points sont correctement définis
on peut afficher dans la partie algèbre les définitions
(afficher les valeurs ne sert pas à grand chose)
ou afficher le protocole de construction avec là aussi les définitions (et éventuellement les descriptions = la traduction en français)
les points A et B servent à définir les rives de la rivière = des parallèles à l'axe des abscisses
tout le reste est construit (lire les définitions)
il n'y a aucun autre point que ceux là à définir nulle part pour cette figure
avec les bons noms des points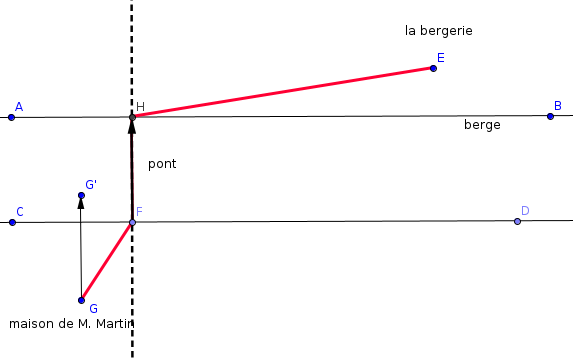
edit> entre temps, mathafou a posté, je laisse quand même le mien avec les légendes  je vous quitte !
je vous quitte !
je postais surtout car kikipopo ne semble pas avoir compris ce qu'est construire quelque chose avec Geogbra
ses points à lui F et H sont du n'importe quoi ; des points placés au pif à peu près
alors que ce doit être les points qu'il a appelé C et D eux mêmes
et qu'il faut renommer en F et H, et pas en créer d'autres ni en ajoutant des points qui ne servent à rien jusqu'à ce que Geogebra en soit aux lettres F et H !
c'est comme ceux qui pour passer à la ligne tapent des espaces jusqu'à ce que ça déborde !
l'intérêt d'une figure sur Geogebra au lieu d'un dessin sur papier est que la figure Geogebra est dynamique alors que celle sur papier est statique.
il suffira de déplacer le seul et unique point F (le vrai) pour que toute la figure suive correctement
alors que son point F est placé à la main au pif (dessiné et pas construit) et donc fixe
quand il déplacera le pont en déplaçant son point C (ce seul point !), son F resterait où il est et la figure alors complètement fausse sans aucun intérêt.
si c'est correctement construit, tout suit automatiquement :

Merci pour vos conseils respectifs.
Il faut que je m'entraîne, mais j'ai peut-être aussi une mauvaise vesrion.
Je n'arrive pas à écrire avec edit. je n'avais pas réussi à dissocier le vecteur de la droite, c'est pour ça que j'ai crée un vecteur à côté.
Je vais chercher auusi comment lier les 3 segements.
Je vais m'entraîner et je reviendrai après.
Merci.
parce que tu cherches bien trop compliqué !
comme le prouve :
Je n'arrive pas à écrire avec edit.
??? quel "edit" ???
pour modifier le nom d'un point c'est un clic droit (clic avec le bouton de droite de la souris) sur le point et un menu apparait :
tu cliques alors (gauche) sur "renommer" etc
fonctionnement de ces "menus surgissant" identique pour tous, absolument tous les logiciels pilotés à la souris, Geogebra ou n'importe lequel autre
je n'avais pas réussi à dissocier le vecteur de la droite, ???
ça ne rime à rien.
justement il FAUT que ce vecteur soit "attaché" aux points de la droite déja crées !
mes figures sont faites avec Goegebra 5 sur PC.
(ou parfois mon vieux Geogebra 4 que je préfère, mais c'est exactement pareil depuis la création de Geogebra)
si tu utilises le Geogebra "en ligne" ![]() du site c'est quasiment pareil.
du site c'est quasiment pareil.
Je ne connais pas ce logiciel. Il y a des manip qui marchent et d'autres pas .
J'ai parlé d'edit parce que je l'ai vu dans une des réponses et que ça existe à deux endroits.
Bref, il faut que je cherche, mais j'y passe beaucoup plus de temps qu'avec ma règle, mon compas et mon crayon (pour la gomme c'est plus rapide !).
Merci.
.
J'ai réussi à faire le schéma et tout bouge d'un seul bloc.
Je n'ai pas réussir l'animation automatique.
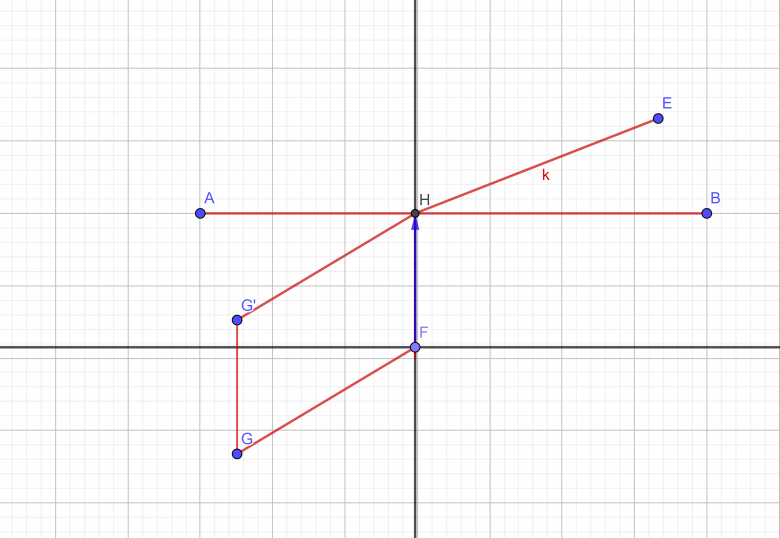

pour l'animation automatique c'est plus compliqué et ce n'est ni demandé ni nécessaire
on peut tout aussi bien bouger à la main et demander d'afficher la longueur GF + FH + HE
pour cela il faut la faire calculer par Geogebra
si les segments s'appellent ainsi (on peut les renommer ou retrouver leur nom dans la construction)
il suffit de taper dans la zone de saisie :
L=GF + FH + HE
pour avoir ce calcul dans la variable L (ou le choix qu'on a décidé de lui donner)
Merci.
La zone de saisie est en bas à gauche ?
Si oui, j'ai saisi L = GH+FH+HE, mais je ne vois pas le résultat .
- si tes segments ne s'appellent pas GH etc, bien sur ... il faut utiliser les vrais noms de tes segments.
- de plus le résultat apparait dans la zone algèbre (en demandant d'afficher les valeurs)
en plus c'est les segments GF, FH et HE
et on est dans la question 1 :
il n'y a aucun vecteur ni point G' à ce stade (pour conjecturer en déplaçant le point et observant les valeurs)
La longueur s'est affichée, mais pour le reste je n'obtiens pas le même affichagr que vous.
Je vais continuer à essayer de comprendre comment fonctionne ce logiciel.
Me ci.
Bonne fin de soirée.
les valeurs sont liées à l'échelle à laquelle tu as fait le dessin et à la position des points fixes (G et E) choisis , la largeur de la rivière etc
chacun a des valeurs différentes vu que aucune donnée numérique sur ces éléments n'est imposée dans l'énoncé
(et de plus quel énoncé ? il y en a plusieurs dans la discussion avec des noms de points différents ...  )
)
ce qui importe est d'observer les variations de la longueur affichée lorsque on déplace le pont HF (le reste restant fixe bien entendu),
pour essayer de "deviner" (conjecturer) à quelle condition cette longueur est minimale.
Bonjour,
Merci.
Oui, effectivement, le résultat sera différent en fonction des valeurs choisies. Pour vous c'est approximativement 13,85
Pour moi (j'ai dû refaire le schéma parce que je ne l'ai pas sauvegardé correctement) le trajet le plus court est lorsque les points GFH sont alignés, ce qui n'est pas le cas pour vous.
"lorsque les points GFH sont alignés" C'est faux
pour qui que ce soit qui fait la manip correctement et quelles que soient les positions et mesures des objets fixes choisis. (la rivière, G et E)
une appli Geogebra toute faite : ![]() (lien vers Geogebra)
(lien vers Geogebra)
la position de la rivière et sa largeur est définie par les points déplaçables A et B
les positions de Martin G et de la bergerie E sont déplaçables à volonté
(contraintes automatiques sur les régions autorisées : impossible de les mettre du même côté ou dans l'eau ni de "retourner " la rivière)
ceci étant fixé
le pont est déplaçable par le point F
diverses positions sont indiquées avec leur longueur
la case à cocher montre la solution (les questions suivantes de l'exo)
(image fixe ici, ça fonctionne sur le site de geogebra, lien ci-dessus)
Bonjour,
Merci beaucoup pour votre aide.
Mon logiciel ne fonctionne pas correctement : ce matin, je ne peux rien saisir dans la zone "saisie".
Je perds beaucoup de temps pour arriver à construire les figures : les outils répondent d'une manière aléatoire
Et quand il fonctionnera, il faudra un minimum d'entraînement pour arriver à votre résultat.
il va falloir que j'achète un Geogebra pour les nuls.
bonne journée
avec quoi donc travailles tu ????
quand tu utilises le site de Geogebra lui même
(j'en rappelle l'adresse donnée le 27-03-21 à 17:15 : ![]() https://www.geogebra.org/classic?lang=fr
https://www.geogebra.org/classic?lang=fr
ce n'est pas ton Geogebra qui tourne, c'est celui qui est à l'intérieur du site de Geogebra (le même pour le monde entier)
si tu as de telles difficultés à faire ça avec un logiciel, fais le sur papier
tu prend UNE (une seule) feuille de papier
tu places la rivière, G et E
une fois pour toutes dessus
tu traces ensuite sur cette unique figure plusieurs emplacements du pont
et tu mesures soigneusement au double décimètre les différents trajets
(la somme des segments GF+FH+HE à chaque fois)
ce sera infiniment moins précis, (et bien moins commode !!) mais ça donne les mêmes résultats.
identique aux valeurs près à ma dernière figure avec plusieurs emplacements du pont sur le même figure statique au lieu d'un pont qui se déplac)
je viens de modifier mon applet sur Geogebra (![]() ) pour qu'on ne puisse pas modifier n'importe quoi n'importe quand
) pour qu'on ne puisse pas modifier n'importe quoi n'importe quand
Une fois choisies la position de la rivière, de G et de E elles ne sont pas déplaçables.
seul le pont l'est vu que le problème est de chercher la position optimale du pont
pas celle de Martin qui est ce qu'elle est.
et si on veut changer les données, le pont disparait vu que au départ il n'y a pas encore de pont !
ça évite de pouvoir répondre :
"l'emplacement du pont est optimal quand on déplace Martin en face du pont " 
(qui serait une question totalement absurde)
Non, je n'ai jamais déplacé Martin en face du pont. J'avais bien compris qu'on ne pouvait que placer au bon endroit l'objet qui permettrait le trajet le pus court qui était à construire et pas déplacer les bâtiments existants.
Mais en déplaçant le schéma en faisant bouger uniquement le pont, c'est lorsque les 3 points étaient alignés que la longueur était la plus courte.
Je me suis connectée au site que vous m'avez indiqué et ça marche mieux. Mais pour arriver à faire un schéma comme le vôtre ça nécessite un peu de travail, ça ne se fait pas automatiquement.
J'ai écrit la somme, mais je n'ai pas mentionné que je voulais qu'on m'indique la plus courte longueur : je ne sais pas comment faire.
tu ne demandes pas à Geogébra de trouver la plus courte longueur
tu observes la longueur que t'affiche Geogebra pour ce trajet et tu cherches en déplaçant le pont, toi, à la main (à la souris), quand est elle la plus courte
et la mesure que l'on doit observer ce n'est pas juste GF (ce serait effectivement au plus court quand GFH alignés : distance d'un point G à la droite de la rive)
c'est la somme
et non tu n'auras jamais le minimum de la somme quand ce sera "en face"
en déplaçant le pont
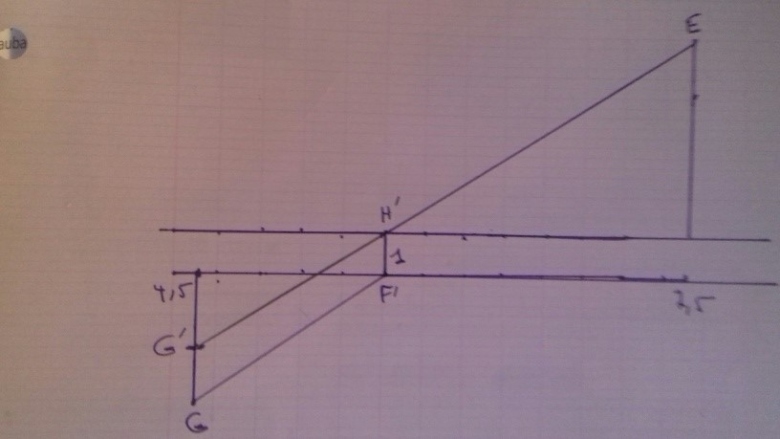
illustration "papier crayon" :
GF = 3, FH = 1, HE = = 13
trajet = 3+1+13 = 17 ("G,F,H sont alignés" seul et unique emplacement du pont où ça se produit)
GF' = = 5, F'H' = 1, H'E=
9.434
trajet 5 + 1 + 9.434 = 15.434 < 17
et il y a même encore un peu plus court : 15.422 en déplaçant le pont de 1/2 cm à droite, tu peux faire le calcul, ça n'utilise que Pythagore
et au delà ça re augmente
et bien entendu le pont est toujours perpendiculaire à la rivière.
ça, c'est rejeté :
(G, F, H alignés, d'accord, mais ce n'est pas l'exo.)
donc je ne sais vraiment pas ce que tu regardes avec Geogebra
autre chose sans aucun rapport très certainement...
je t'ai deja conseillé de faire la manip avec papier crayon et de laisser tomber Geogebra pour avancer dans l'exo (on est seulement à la question une !!)
Si on déplace le pont de 0,5 cm à droite,
GF' = =5,4
H'E = =9,01
F'H' =1
GF'+F'H'+H'E = 15,41
2 )construction du point G' par translation de F' en H' et constrution du parallélogramme
GG'H'F'
1) on pourra faire tous les calculs que l'on veut, que ce soit à la main où avec Geogebra, cela ne serait jamais fini (les nombres réels sont en nombre infini)
on n'obtiendra que uniquement une conjecture :
il semble que avec ces données là ce soit à cet emplacement là
et que ce qui caractérise "à l'oeil" (conjecture !!) ce qui semble être la meilleure position est lorsque les segments GF et HE sont à peu près parallèles.
(voir ça sera bien plus long à la main en faisant des dizaines de figures et de calculs / mesures au double décimètre que avec Geogebra bien entendu
sans même parler de facultés d'observation)
2)
Il est très important de ne pas se placer dans un cas particulier mais dans le cas général.
sinon il sera impossible de raisonner sur quoi que ce soit.
G' - H- E alignés est un cas particulier à éviter pour pouvoir faire un raisonnement :
que quelle que soit la position du pont , le trajet GFHE a même longueur que le trajet GG'HE
etc.
nota : tes calculs sont approchés
dans des calculs on doit toujours attendre seulement à la toute fin du calcul pour arrondir et ne jamais arrondir "en cours de route"
et seulement maintenant on arrondit à 15.42
bien entendu on ne retape pas ces nombres à rallonge ! (ici avec la calculatrice de Windows)
on les laisse tels qu'ils sont dans la calculette sans rien re-taper : toutes les calculettes ont une fonction de mémoire et de mise entre parenthèses pour enchainer les calculs
voir où exactement est le vrai minimum n'est pas possible avec une telle technique
c'est quoi qu'on fasse "à peu près", même avec des calculs à 30 décimales. on ne sera jamais certain que c'est vraiment le minimum avant d'avoir terminé la question 3 qui donne l'emplacement exact.
la question 2 montre que
quelle que soit la position du pont , le trajet GFHE a même longueur que le trajet GG'HE
donc le trajet minimum sera quand G'H + HE sera minimum
(GG' est constant)
et G' est fixe
alors quelle est la position de H qui rend minimale la distance G'H+HE ?
c'est niveau début de collège : la plus courte distance entre deux points (entre G' et E) est ...
Bonjour,
J'avais répondu hier soir, mais mon message n'est vraisemblablement pas parti.
La distance la plus courte entre 2 points est la ligne droite.
C'est donc quand G'HE sont alignés que la distance est la plus courte et puisque GF = G'H
c'est dans cette position G'HE que la distance GFH'E est la plus courte.
voila
(il semble qu'il y ait eu quelques soucis sur le site, au vu d'autres messages.
tout semble en ordre ce matin ...? )
et donc la construction demandée :
on décale G de la largeur de la rivière en G',
on trace la droite G'E
etc.
et si on veut faire des calculs de cet emplacement : un coup de Thalès avec la construction précédente
bein ceux là pardi
on cherche la position de Hmin, donc la distance CHmin
on connait les distances de la bergerie à la rivière ED (c'est des données, même si elles ne sont pas connues ici, c'est toi qui les a choisies en choisissant la position de E)
de Martin à la rivière G'C
et la distance CD le long de la rivière
Merci.
Donc on ne peut pas résoudre ce problème sans les hypothèses trouvées avec geogebra.
j'aimerais bien savoir comment poser l'équation ou l'inéquation qui permette de trouver la plus petite distance entre G et E en passant FH sans connaître la position.
C'est sûrement une fonction du second degré avec un extremum.
les seules valeurs que je connais sont celles que j'ai choisies sans savoir si le pont est correctement placé. Je ne sais pas si ce que je dis est clair.
n'importe quoi.
question 1) Gêogebra permet de faire une conjecture ... ou PAS du tout
comme tu n'as pas réussi à utiliser correctement Geogebra tu n'as pas pu faire de conjecture du tout, que seulement prétendre des trucs faux dû à ta mauvaise utilisation de Geogebra : que G, H, F seraient alignés
à défaut de Géogebra je t'ai proposé de remplacer cette question 1 par des calculs sur des figures papier
en vrai il n'y a aucun calcul à faire dans cet exo.
que exclusivement de l'observation (donc si on n'est pas suffisamment observateur , et bien on ne verra rien non plus, même avec Geogebra)
question 2) ce qu'on a trouvé ou pas question1 ne sert à rien du tout.
cette question 2 est le début guidé (tracer G' et le parallélogramme) d'une détermination exacte avec preuve de la solution (de la vraie solution, pas d'un truc trouvé à la boule de cristal = conjecturé)
cela aboutit (par uniquement un raisonnement géométrique sans aucun calcul sur "la plus courte distance est la ligne droite"
ou équivalent en plus "savant" : l'inégalité triangulaire
dans tout triangle un coté (G'E) est inférieur à la somme des deux autres (G'H+HE)
et la solution :
point barre.
question 3)
"en déduire" une construction :
construire G', translaté d'un vecteur représentant la largeur de la rivière
tracer G'E
elle coupe la rive coté bergerie en H
terminer le construction (F puis les segments)
en utilisant cette construction on peut observer que cela correspond à ce qu'on avait conjecturé question1
exercice terminé
il n'y aucun calcul à faire
pour aller plus loin
et remplacer l'observation de Géogebra que tu ne peux pas faire
je te proposais des calculs donnant les mêmes conclusions :
calculer avec Thalès sur la construction faite la position de Hmin
(que ce que j'avais dit : le minimum est 0.5 plus à droite de H' sur cette figure là d'exemple
c'est à dire que G'E coupe bien la rive à cet endroit là exactement