Inscription / Connexion Nouveau Sujet
géométrie optimisation
Bonjour
Je bloque sur mon exercice de géométrie depuis une heure alors j'ai besoin de votre aide
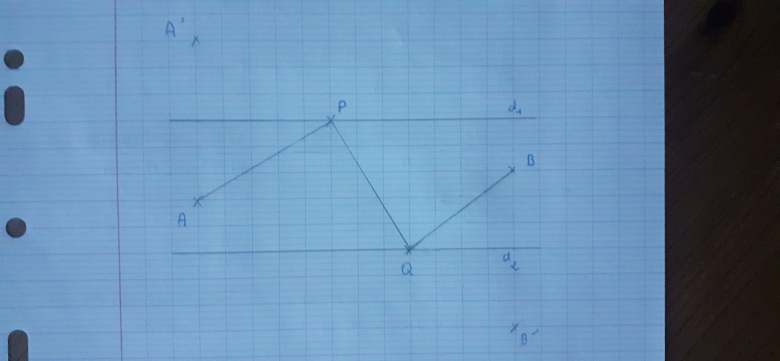
d1 et d2 sont parallèles . P appartient à d1 et Q appartient à d2. A est à gauche de P et Q entre d1 et d2. B est aussi entre d1 et d2 à droite de Q et P.
1/ J'ai réussi à tracer le symétrique de A et B comme demandé. A' symétrique de A par rapport à d1 et B' symétrique de B par rapport à d2
2/ En déduire la position de P et Q pour que AP + PQ + QB soit minimal.
C'est la que je coince.
Il faut se servir de A' et B' selon moi. Dc on a des triangles isocèles . J'ai aussi appris que le projeté orthogonal est la distance minimal J'ai pensé que P et Q doivent être en face pour que PQ soit minimal. Mais si AP est minimal quand A ou P est le projeté orthogonal ça marche pas P n'est pas en face de Q.
Merci si vous pouvez me donner des pistes pour me débloquer. Est ce qu'il faut bien partir sur les projetés orthogonaux?
Bonjour
cela ne ressemble pas à un véritable énoncé, mais à un énoncé raconté
quel est le véritable énoncé ? y-avait-il une figure, si oui la mettre
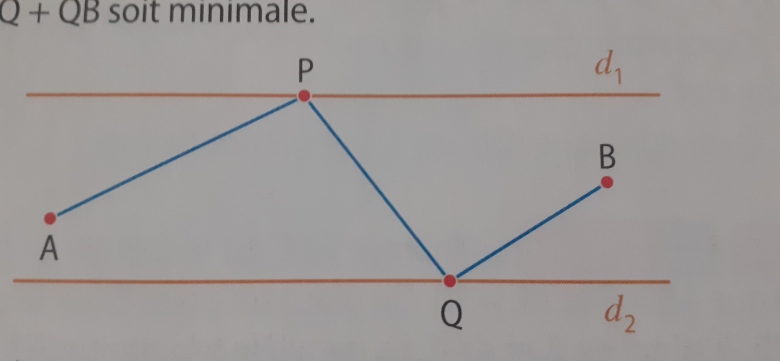
Sur la figure ci-dessous, d1 et d2 sont 2 droites parallèles. On cherche à placer les points P et Q de telle sorte que la longueur AP + PQ +QB soit minimale.
1/ Reproduire la figure et construire A' symétrique de A par rapport à d1 et B 'de B par rapport à d2.
2/ En déduire la construction de P et Q tels que AP + PQ +QB soit minimale.
bonjour,
tu as construit A' et B' ?
si oui, tu peux poster ta figure.
Ensuite, je t'aiderai pour répondre à la question.
OK, trace A'B', tu y verras plus clair.
on veut minimiser AP + PQ +QB ,
à ton avis, par quoi peut on remplacer AP et QB ? (ton idée d'utiliser A' et B' est bonne).
Par A'P et B'Q?
oui, donc minimiser AP + PQ +QB , revient à minimiser A'P + PQ + QB'
n'oublie pas de préciser pourquoi AP=A'P et pourquoi BQ = B'Q ...
ensuite tu dis : " Pour moi c était quand A'PQ et B étaient alignés ms j arrive pas à le prouver"
que veux tu "prouver" ?
dans ton cours , quelle est la distance la plus courte entre deux points A' et B' ?
Donc si j'ai bien compris je montre que PA=PA' et QB=QB'
Puis je dis que chercher PA+PQ+QB minimal c'est comme chercher PA'+PQ+QB' minimal
Or le chemin le court pour relier 2 points est une droite.
donc PA'+ PQ+QB' est minimal quand les points A', P, Q et B' sont alignés
et je peux faire la figure pour placer P et Q.
c'est tout a fait ça !
" en déduire la construction de P et Q", ce que tu es capable de faire maintenant 
Tu as d'autres questions ?
salut
une remarque : quand on dit
1/ Reproduire la figure et construire A' symétrique de A par rapport à d1 et B 'de B par rapport à d2.
et tu complèteras ta figure avec les "bons" points P et Q