Inscription / Connexion Nouveau Sujet
Géométrie plane
bonjours tousle monde j'ai un exercice que je n'arrive pas à faire pouriez ous m'aider merci d'avance
ACE est un triangle. S et R sont les points tels que : vecteur SC= -3vecteur SE et vecteur AR = 1/4vecteur AC
le point B est le milieu du segment [AE]
En utilisant le repère (A; vecteur AE; vecteur AC)démontrer que les droites (AS) , (RE) et (CB) sont concourantes
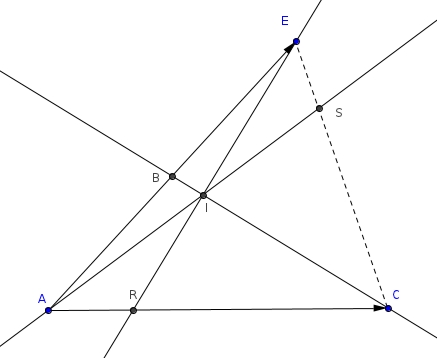
J'ai fait la figure sur géogébra on voit bien que les 3 droites se coupent en un même point mais je ne sais pas comment le prouver
Merci d'avance
Trouve les coordonnées du point d'intersection de deux d'entre elles et vérifie que ce point est sur la troisième
* = vecteur ça sera plus facile 
j'ai chercher *CB et *RE en fonction de *AE et *AC
*CB= -*CA + 1/2*AE
*RE= *AE + 1/4 *AC
Par contre je ne sais pas comment je peux trouver les coordonnée de croisement de ces points :$
tu as au moins quatre manières de faire, vectorielle, barycentres, colinéarité ou équations de droites
je te propose la dernière, mais je ne sais pas si tu as déjà vu la technique...
Dans le repère
A a pour coordonnées
Tu as calculé, enfin j'espère, que
S a pour coordonnées
La droite (AS) a pour équation
C a pour coordonnées
B a pour coordonnées
La droite (BC) a pour équation
En résolvant le système
on trouve la solution
ce sont les coordonnées du point d'intersection I des deux droites (AS) et (BC) dans le repère
E a pour coordonnées
R a pour coordonnées
La droite (ER) a pour équation
nous vérifions qu'en remplaçant x et y par les coordonnées de I, l'équation de la droite (ER) est vérifiée
Ce qui est la preuve que I est aussi sur cette droite.
Merci beaucoup pour ta réponse effectivement je n'ai pas encore vu cette méthode désoler de t'embéter mais comment peux tu faire en utilisant la méthode des barycentre ?
Merci d'avance
tu es courageux
ce n'est pas la technique préférée des élèves
Rappels
si , alors l'équation
a une solution unique G, appelée barycentre de (A,a),(B,b)
On peut étendre ceci à un ensemble plus nombreux de points dits pondérés
Alors on rappelle aussi que
G barycentre de (A,a),(B,b),(C,c) vérifie l'équation
Voici le principe de substitution des barycentres :
Si G barycentre de (A,a),(B,b),(C,c) et H barycentre de (B,b),(C,c) alors
G barycentre de (A,a),(H,b+c)
L'inverse est vraie aussi
Si G barycentre de (A,a),(H,b+c) et H barycentre de (B,b),(C,c) alors
G barycentre de (A,a),(B,b),(C,c)
Autre propriété à connaître :
Pour tout point I d'une droite (AB) il existe au moins un couple (a,b) tel que I est barycentre de (A,a),(B,b)
Tous les autres couples sont proportionnels à celui-ci
On y va
donc
donc
S barycentre de (C,1),(E,3)
B milieu de [AC] donc
B barycentre de (A,1),(C,1)
donc
R barycentre de (A,3),(C,1)
Soit alors I intersection des droites (AS) et (ER)
il existe (a,s) tel que
I barycentre de (A,a),(S,s)
il existe (e,r) tel que
I barycentre de (E,e),(R,r)
On substitue (S,s) par (C,),(E,
) : la somme s/4+3s/4 reste s, et les coefficients sont proportionnels à 1,3 qui sont les masses qui définissent S comme barycentre de (C,1),(E,3)
il existe (a,s) tel que
I barycentre de (A,a),(C,),(E,
)
on fait de même en substituant (R,r) par (A,),(C,
)
I barycentre de (E,e),(A,),(C,
)
on réordonne et on compare
I barycentre de (A,a),(C,),(E,
)
I barycentre de (A,),(C,
),(E,e)
Mais alors les masses de ces systèmes de points ayant même barycentre sont proportionnelles
en particulier j'exprime la proportionnalité des coefficients de A et C
, car dans le cas contraire I serait confondu avec E, or E n'est pas sur la droite (AS)
donc il reste
donc
I barycentre de (A,),(C,
),(E,
)
mais on peut substituer (A,),(E,
) par
(les masses de A et E sont identiques, donc on utilise B milieu de [AE], affecté de la somme des deux masses)
I barycentre de (B,),(C,
)
et donc I est aussi un point de la droite (BC)


