Inscription / Connexion Nouveau Sujet
Géométrie Plane - Spatiale.
Bonjour à tous !
J'ai un devoir maison à faire mais je rencontre des difficultés..
Exercice :
Sur la figure ci-contre, le trait plein représente le bord d'une chaussée à un carrefour. La partie courbe est constituée de deux arcs de cercle de centre O et O'. L'arc de cercle de centre O' et l'arc de cercle de centre O sont tangents aux bords des chaussées respectivement T1 et T3. De plus, ils admettent en T2 une tangente commune (S1 S2 ). Une instruction officielle fixe pour chaque valeur de l'angle formé par les deux voies ( que l'on nomme " déviation " ) les rayons minimaux des deux cercles, afin qu les semi-remorques puissent tourner facilement. Pour une déviation de 120° ( c'est le cas ici ), on lit : O'T1 = 11 m ; OT3 = 75 m ; HT3 = 14 m. Le point S étant connu, le but de l'exercice est de : calculer les distances ST1 et ST3.
Toutes les distances sont exprimées en mètres à 10-2 près et les angles en degrés à 10-2 près.
1) Calculer une mesure de l'angle T2OT3.
En déduire une mesure de l'angle T2S2T3 puis une mesure de l'angle T1S1T2.
2) Calculer les distances S2T3 et S1T1. En déduire S1S2.
3) Calculer les distances SS1 et SS2. En déduire les distances ST1 et ST3.
( Réponses : ST1 
22,52 m ; ST3 40,15m )
Voilà. Merci d'avance ! J'ai quelques calculs etc je vais mettre le schéma. C'est une photo que j'ai faite donc pas super qualité.. Merci !
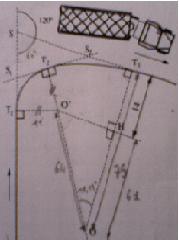
Première partie de la question 1).
On sait que [O'T1] = 11m, [OT3] = 75m, [HT3] = 14m
A partir de ces données on peut en déduire que :
[OH] = [OT3] - [HT3] = 75 - 14 = 61m
De plus, on sait que la tangente (S1S2) est commune aux arcs de cercle O et O'
On en déduit que [O'T1] = [O'T2] et [OT2] = [OT3]
Donc [O'T2] = 11m
et [OT2] = 75m
Alors [OO'] = [OT2] - [O'T2] = 75 - 11 = 64m
cos Ô = [OH] / [OO']
cos Ô = 61 / 64
Ô = arccos (61 / 64)
Ô = 17,61°
Bon courage pour la suite, j'aurai bien mis la partie 2 et la partie 3 de la question 1) mais je ne sais pas si mes résultats sont correctes :-/
Merci d'avoir répondu !
Alors pour la première partie de la question 1 j'avais fait exactement ça. Mais je galère pour trouver l'angle T2S2T3. :/
J'veux bien te donner ce que j'ai trouvé, mais j'suis pas sûre du tout du résultats, ni de mon raisonnement :-S
En fait grâce à cette angle on détermine facilement le troisième angle demandé .. Mais je trouve un résultat qui ne colle pas avec le schéma .. (Sur le schéma angle < 90, avec mon calcul je trouve un angle > 90 :/)
Comme (S2T2) et (S2T3) sont deux tangentes du cercle de centre O et qu'elles se coupent en un point S2,
Alors [T2S2] = [S2T3]
et l'angle T2OS2 = l'angle S2OT3 = l'angle T2OT3 / 2 = 8.80°
De plus, l'angle T2S2T3 = 2* l'angle T2S2O
180 = T2S2O + S2T2O + T2OS2
T2S2O = 180 - 90 - 8,80 = 81,20°
T2S2T3 = 2* T2S2O = 2*81,20 = 162,40°
Après reste à vérifier si mon raisonnement est correcte ...
J'ai tout compris ! Tu es très explicite merci ! 
Et tu as dit que sur le schéma tu as vu un angle < à 90° et tu trouves un angle > à 90° tu parles de quel angle ?
C'est Maxime 
?
Bah, celui tout à gauche, SS1T2
En faisant 180 - 60 - (180 - 162,40) on trouve un angle plus grand que 90° .. :/
Hm, désolé, en fait un camarade de classe avait l'intention de poster le sujet, on a le même DM à faire pour mardi alors quand j'ai voulu taper le sujet sur google, pour vérifier ce que j'avais fait j'suis tomber sur ton post ..
Voilà, donc je sais pas trop où est la faute, sûrement dans mon raisonnement, je sais pas :/, sa me paraissait pourtant juste, mais en regardant l'angle sur le schéma j'ai un gros doute x)
Annuler
connectez vous