http:/*******

Bonjour,

Je t'aide pour le début :
Pose AM = x, alors MB = 10-x
La surface du carré AEMF est :
S1 = x²
C'est un peu pluus compliqué pour la surface du triangle MBG :
MB est l'hypothénuse du triangle. Dans ce triangle, on a :
GM = GB
MB = GM2 = GB2
D'où GM = GB = MB/2 = (10-x)/2
Et la surface du triangle MBG est :
S2 = (1/2)GM*GB = (1/2)((10-x)/2)² = (1/2)(10-x)²/2 = (10-x)²/4
Et donc :
S1+S2 = x²+(10-x)²/4 = (4x²+100-20x+x²)/4 = (5x²-20x+100)/4 = (5/4)(x²-4x+20)
A partir de là, tu devrais pouvoir avancer...

Franchement merci beaucoup , tu m'a beaucoup aidé avec ton raisonnement mais comment je vais savoir que cest l'aire minimale

Il faut trouver le minimum de x²-4x+20, je ne sais pas ce que vous avez comme outil pour cela en seconde : calcul de la dérivée ? tracé graphique de courbe ? Pour t'aider, je te donne le résultat, le minimum est atteint en x = 2.

merci beaucoup
je venais de comprendre aussi qu'il fallait trouver le minimum de S2 mais je ne savais pas comment y arriver
Mais maintenant c'est bon merci beaucoup

Et pour le b) il faut que l'aire de S1 ET S2 soit supérieure à racine de 50 vu que le carré est de côté de 10 cela fait 100 pour l'aire du carré .

c'est ça ou pas ?

Bonjour,
pas de lien vers un scan
seule l'image utile peut être insérée la procédure est ici

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

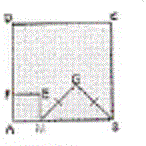
L'aire du carré est 10*10 = 100. Sa moitié est dont 50.
Tu dois donc trouver x tel que :
(5/4)(x²-4x+20) > 50
x²-4x+20 > 50*4/5 = 40
x²-4x-20 > 0
A nouveau, je ne sais pas ce que vous avez comme outil pour cela en seconde.
La solution est approximativement 6,899.

Merci encore une fois
mais il y a une chose que je ne comprend comment tu trouves (4x²+100-20x+x²)/4 comment on passe de x² à 4x²

Simplement en réduisant tout au même dénominateur dans  l'esprerssion S1+S2 = x²+(10-x)²/4

Bonjours aujourd'hui je me retrouve avec le même devoir et je bloque même avec vos informations je bloque ... Merci si dès personnes prennent le temps de m'aider 😓

Bonjour Skratt,
tu auras plus de chances d'avoir des réponses si tu postes ton propre message au lieu de poser ta question dans un topic vieux de 2 ans.....