Inscription / Connexion Nouveau Sujet
Graphe : l'algorithme de Dijkstra
Bonjour,
J'aurais voulu savoir si ce que j'ai fais est correct.
"En utilisant l'algorithme de Dijkstra, déterminer le trajet qui minimise le temps de parcours pour aller de E à S."
J'ai trouvé grâce à l'algorithme de Dijkstra que le plus court chemin allant de E à S a pour longueur 21 et est EBACFDHKS.
Merci.
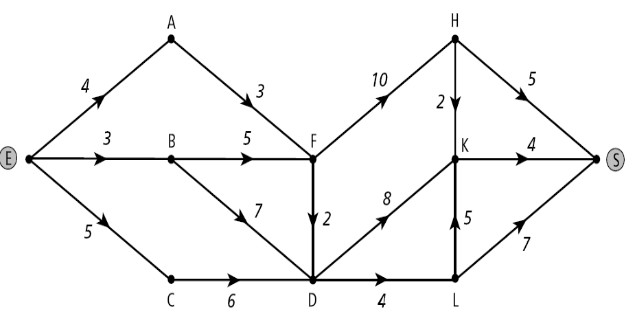
Bonjour,
Il y a un problème, c'est que EBACFDHKS n'est pas du tout un chemin 
!
Revois ton algorithme, vous avez sûrement détaillé un exemple en cours ?
Non, nous avons pas vu cela en cours ; c'est pour cela que je demande de l'aide, un petit coup de pouce, une explication pas à pas. Merci
Trouvé ça 
avec un exemple à la fin (en cliquant sur le bouton "algorithme de Dijkstra" l'algorithme se déroule pas à pas.)
Avant de faire un autre exercice pour continuer à progresser, j'aurais voulu de l'aide pour l'exercice posté car accumuler les exercices sans réussir cela ne sert strictement à rien. De plus, le mien étant plus complexe car il y a des fléches.
Est-ce que le plus court chemin est EBDLS de longueur 21. Est-ce correct ? Merci
Bon j'ai fait un tableau aussi, sur le même principe que celui que tu as utilisé, je trouve :
| E | A | B | C | D | F | H | K | L | S | sélect. |
| 0 |  | | | | | | | | | E |
| . | 4(E) | 3(E) | 5(E) | | | | | | | B |
| . | 4(E) | . | 5(E) | 10(B) | 8(B) | | | | | A |
| . | . | . | 5(E) | 10(B) | 7(A) | | | | | C |
| . | . | . | . | 10(B) | 7(A) | | | | | F |
| . | . | . | . | 9(F) | . | 17(F) | | | | D |
| . | . | . | . | . | . | 17(F) | 17(D) | 13(D) | L | |
| . | . | . | . | . | . | 17(F) | 17(D) | . | 20(L) | H ou K |
| . | . | . | . | . | . | . | ||||
| . | . | . | . | . | . | . |
À la fin on trouve deux sommets qui ont un poids minimal (H et K), donc il faut regarder ce qui se passe dans chaque cas (fais avec deux couleurs différentes dans ton tableau sur papier, par exemple).
On trouve au final que le plus court chemin arrivant en S est de longueur 20. Comme indiqué dans "20(L)", on est arrivé en S en venant de L.
--> la fin du chemin est LS
Par où est-on arrivé en L ? réponse dans la colonne de L : "13(D)", donc on venait de D
--> la fin du chemin est DLS
En continuant ce raisonnement on trouve bien EAFDLS.
Zut il y a un décalage dans une ligne de mon tableau vers la fin... évidemment le n'a rien à faire à côté de "13(D)", il appartient à la colonne suivante, idem pour le L qui doit être dans la colonne des sommets "sélectionnés".
!
Annuler
connectez vous