Inscription / Connexion Nouveau Sujet
Groupes algèbre
Bonsoir à tous!
Notre prof nous a donné une dizaine de démonstrations du cours à faire nous-mêmes et il y en a deux sur lesquelles je sèche réellement:
Pour le 1) :
H et K sont engendrés par des parties x et y, et Z inclus dans G.
Pour le 2)
Il faut montrer l'égalité, en montrant la double inclusion.
Pour un sens de l'inclusion c'est bon, pour l'autre sens,c'est pas bon!
Voilà
Un grand merci a qui pourra m'aider
était la signature 
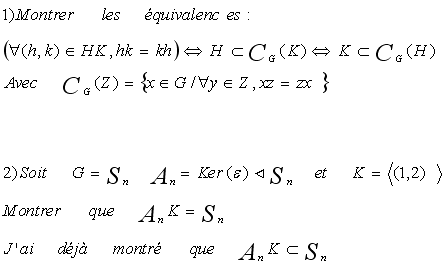
Bonsoir lolo5959;
Pour l'exercice 1) les trois propositions dont on te demande de montrer l'équivalence ne font qu'une tu n'as qu'à les exprimer par des phrases pour t'en convaincre.
En effet on a que:
(*)la proposition est équivalente à dire que tout élément de H commute avec tout élément de K.
(*)la propostion est équivalente à dire que H fait partie de l'ensemble des éléments de G qui commutent avec tous les éléments de K.
(*)et la proposition est équivalente à dire que K fait partie de l'ensemble des éléments de G qui commutent avec tous les éléments de H.
C'est comme si on te demande de prouver que
Pour l'exercice 2) c'est plutot du cours puisqu'on sait que pour l'application signature
est un morphisme surjectif du groupe symétrique
(groupe des permutations d'un ensemble
à
éléments) dans le groupe
et comme le noyau de ce morphisme est justement
(groupe des permutations paires ou positives appelé aussi groupe alterné) on voit qu'il est distingué dans
et d'indice
et donc qu'en particulier on a
Donc si tu prends n'importe quel élément de (par exemple la transposition
) l'application
étant clairement injective est une bijection (puisque les ensembles de départ et d'arrivée sont finis et ont m^me nombre d'éléments) et donc qu'en particulier toute permutation impaire est la composée d'une permutation paire et la transposition
ce qui s'écrit aussi
d'où si
désigne le sous groupe de
engendré par la transposition
on a que
et comme on a aussi que
on voit que
et l'autre inclusion étant acquise tu as le résultat souhaité.
Sauf erreurs bien entendu 
Merci bien elhor_abdelali pour l'aide que vous m'apportez.
Pour revenir au 1), je suis tout à fait d'accord que cela revient au même, mais c'est justement ça que notre prof nous a demandé de montrer: Pourquoi "tout télément de H" est égal à "H fait partie de l'ensemble des éléments de G".
Je disais que c'est paske H est inclus dans G mais il a dit que c'était "plus fin" que ça et que je ne montrais rien en disant ça, alors voilà, y'a vraiment pas moyen de le montrer ? 
En tout cas encore merci pour l'aide ( en pleine nuit en plus
)
Annuler
connectez vous
algèbre en post-bac