Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... BTSForum de maths BTS GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau BTS
Partager :

Intersection de deux cercles

Posté par Dogbolter (invité) 20-12-04 à 12:18

Bonjour,

Je suis à la recherche de la formule qui me permettrait de déterminer les coordonnées x,y,z des points d'intersection entre deux cercles sachant que l'on connait les deux centres et les rayons...
D'avance merci

Posté par
Nightmarere : Intersection de deux cercles 20-12-04 à 12:52

Bonjour

Soit C ton premier cercle de centre (a;b) et de rayon r , alors celui ci a pour équation :
(x-a)^{2}+(y-b)^{2}=r^{2}

Soit D ton deuxiéme cercle de centre (c;d) et de rayons s , alors il a pour équation :
(x-c)^{2}+(y-d)^{2}=s^{2}


Pour trouver leur points d'intersection , il te suffit de résoudre le systéme :
\{{(x-a)^{2}+(y-b)^{2}=r^{2}\\(x-c)^{2}+(y-d)^{2}=s^{2}}\
(Cela peut paraitre compliqué mais je rapelle que a , b , c , d , r et sont connues , nous avons seulement x et y comme inconnues )


Jord

Posté par Dogbolter (invité)re : Intersection de deux cercles 20-12-04 à 13:19

Tout d'abord merci pour la réponse si rapide.

En fait c'est la solution finale qui m'intéresse...
Pas trop le temps de résoudre le système.
Le but étant de l'intégrer dans un programme,il me faudrait x= et y= .

D'avance merci

Posté par
Nightmarere : Intersection de deux cercles 20-12-04 à 13:20

Bon alors en fait je viens de me rendre compte que c'est pas si simple que ca

Enfin je te montre la résolution tu pourras me dire ce que tu en penses

\{{(x-a)^{2}+(y-b)^{2}=r^{2}\\(x-c)^{2}+(y-d)^{2}=s^{2}}\

En développant , le systéme revient a :
\{{x^{2}-2ax+a^{2}+y^{2}-2by+b^{2}=r^{2}\\x^{2}-2cx+c^{2}+y^{2}-2dy+d^{2}=s^{2}}\

En soustrayant la ligne 2 a la ligne 1 :
s^{2}-r^{2}=c^{2}-a^{2}+2x(a-c)+d^{2}-b^{2}+2y(b-d)
Soit :
2y(b-d)=s^{2}-r^{2}-c^{2}+a^{2}-2x(a-c)-d^{2}+b^{2}
et encore :
y=\frac{s^{2}-r^{2}-c^{2}+a^{2}-d^{2}+b^{2}}{2(b-d)}-x\(\frac{a-c}{b-d}\)

Posons :
M=\frac{s^{2}-r^{2}-c^{2}+a^{2}-d^{2}+b^{2}}{2(b-d)}
Nous avons alors :
y=M-x\(\frac{a-c}{b-d}\)
soit :
y^{2}=M^{2}+x^{2}\(\frac{a-c}{b-d}\)^{2}-2Mx\(\frac{a-c}{b-d}\)

On obtient :
r^{2}=a^{2}+x^{2}-2ax+b^{2}+M^{2}+x^{2}\(\frac{a-c}{b-d}\)^{2}-2Mx\(\frac{a-c}{b-d}\)-2bM+2bx\(\frac{a-c}{b-d}\)

D'ou au final :
x^{2}\underb{\[\(\frac{a-c}{b-d}\)^{2}+1\]}_{A}+\underb{x\[2b\(\frac{a-c}{b-d}\)-2M\(\frac{a-c}{b-d}\)-2a\]}_{B}+\underb{\[a^{2}+b^{2}+M^{2}-r^{2}-2bM\]}_{C}=0

On se retrouve alors face a une équation du second degré :
Ax^{2}+Bx+C=0

Long , mais pas si compliqué lorsqu'on a a , b , c , d , r et s


Jord

Posté par Dogbolter (invité)re : Intersection de deux cercles 20-12-04 à 14:47

Mille merci........
C'est exactement ce que je cherchais...

A plus

Posté par
Nightmarere : Intersection de deux cercles 20-12-04 à 14:52

Pas de probléme


Jord

Posté par
JJare : Intersection de deux cercles 20-12-04 à 15:10

:

Intersection de deux cercles

Posté par
J-P Posteur d'énigmesre : Intersection de deux cercles 20-12-04 à 18:04

Je suppose que les cercles étaient coplanaires, en lisant l'énoncé ce n'est pas évident puisqu'on parle des coordonnées x,y,z des points de rencontre des cercles.

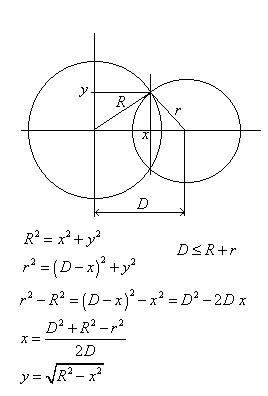
Posté par Dogbolter (invité)re : Intersection de deux cercles 22-12-04 à 16:52

Salut et encore merci,

Il s'agit bien de deux cercles coplanaires c'etait pour un prog de triangulation...
Tout fonctionne parfaitement
Il est vrai que l'on a comencé avec x,y,z sous entendu z constant.

A plus


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !