Inscription / Connexion Nouveau Sujet
Intersection de deux plans
Bonjour,
on me demande de tracer l'intersection des plans (MNP)et (CGH) ici. Je l'ai représenté en orange merci de me dire si c'est correct
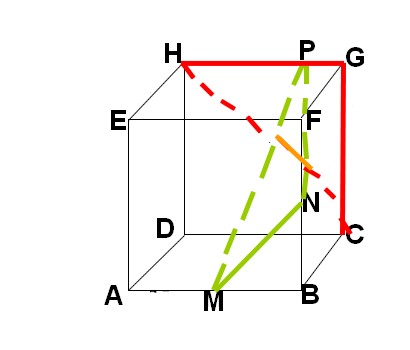
si on peut deviner sans trop de risque pour les autres points, j'ai quant à moi du mal à savoir comment est défini N
ha, N est le milieu du segment
et P, comme dit pegase ? un point (mobile) du segment [HG], je suppose
donc le trait orange ne représente pas l'intersection des deux plans, c'est certain.
bonjour
un plan coupe 2 plans parallèles suivant 2 droites parallèles
(MN) (ABFE) parallèle à (DCGH)
(ABFE) parallèle à (DCGH)
donc je commencerais par tracer la parallèle à (MN) passant par P.
je vous laisse joindre des belles figures! 
ben non j'assume pas
moi je tracerais cette parallèle à (MN) passant par P . Elle coupe (AE) en Q.
ensuite on trace (QM) et on a notre intersection
allez je te laisse la main dhalte si tu veux bien 
tu étais sur la bonne piste, mais la parallèle à (MN) est dans le plan arrière, et coupe (DH), pas (AE)
alors appelons Q ce point de [DH]
je ne pense pas qu'il suffise de joindre (MQ) pour finir l'exercice!
je te laisse la main et merci de ton aide qui nous aura servi à tous les 2
vive 
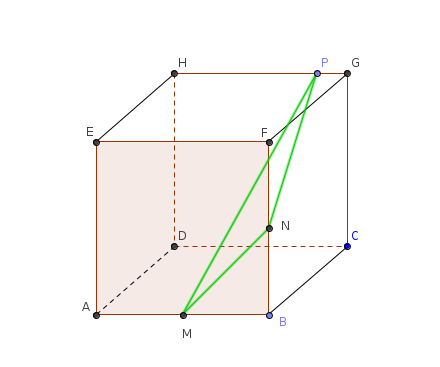
ABFE et DCGH sont deux plans parallèles
(MN) est dans le premier plan
P est dans le second
le plan MNP coupe ces deux plans parallèles selon deux droites parallèles
imagine la table de la cuisine comme le plan MNP, et la cuisine comme un cube, fais bouger la table (expérience de pensée, hein, pas de blagues) et imagine prolonger la table jusqu'aux murs opposés : ce plan de travail coupe ces murs opposés suivant deux droites parallèles
(MN) est la droite commune à la face ABFE
la seconde passe par P et est donc parallèle à (MN), et bien sûr est contenue dans (DCGH)
voilà pourquoi on peut tracer sur le graphique cette parallèle à (MN) passant par P, et elle coupe (DH) puisque elles sont toutes deux dans ce plan (DCGH)
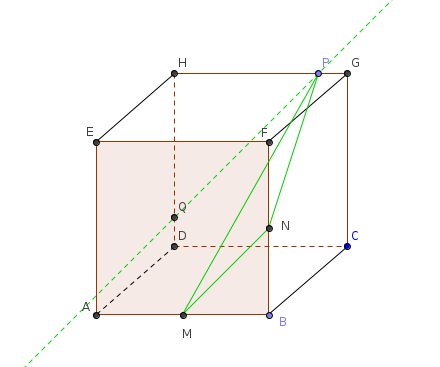
ben tu peux déjà mettre à jour ta figure en traçant la parallèle à MN passant par P
le plan (MNP) contient (MN)
MNP coupe (ABFE) suivant (MN)
MNP coupera donc (DCGH) suivant une droite parallèle à (MN)
or MNP contient P. donc (MNP) coupe (DCGH) en (PQ) la parallèle à (MN) passant par Q
Q appartient à (HD)
joins 1 figure qui montre tout ça
plus de nouvelles
je pensais que le problème continuerait logiquement par la recherche des autres intersections de ce plan avec les faces du cube
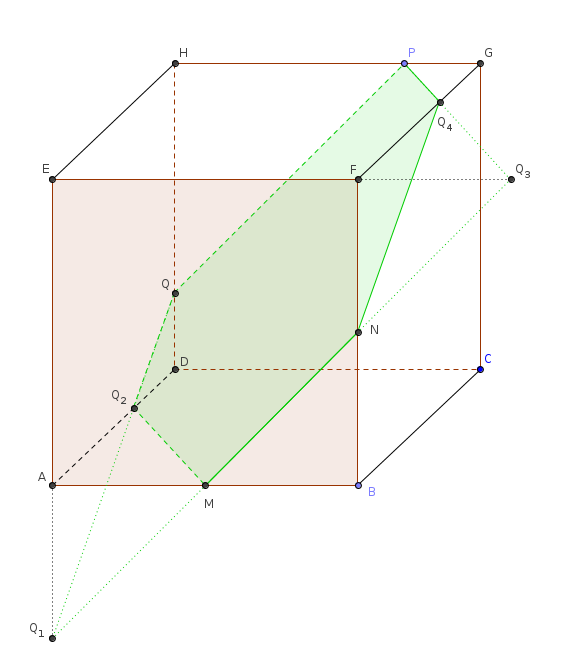
dommage, je sentais fedjer prêt à faire des étincelles.
toujours aussi moqueur! 
ben non pas d'étincelles. dans l'espace je n'arrive pas à dépasser le cap des plans parallèles.
je n'aurais pas pensé tracer l'intersection de (MN) et (EA)

donc pour résumer l'intersection des deux plans est la droite (PQ) car c'est juste ça qu'on demandait
mais non c'est tout le plan délimité par les droites MN NQ4; Q4P;...
le plan coupe chacune des faces du cubes suivant des droites qu'il faut trouver
oui mais ton cube n'est pas 1 plan mais 6 plans
on doit tracer l'intersection du plan avec chacune des 6 faces du cube!
Effectivement, l'intersection des plans (MNP) et (CGH) est la droite (PQ).
L'intersection du plan (MNP) et des faces du cube n'était apparemment pas demandée.
L'intersection du plan (MNP) et des faces du cube n'était apparemment pas demandée
effectivement dans l'énoncé du premier message de manon430
et c'est bien pour cela que j'ai indiqué :
je pensais que le problème continuerait logiquement par la recherche des autres intersections de ce plan avec les faces du cube




