Inscription / Connexion Nouveau Sujet
intersection de deux polygones convexes a coordonnées entière
Bonjour,
je cherche un un algorithme qui permet de calculer l'aire d'intersection entre deux polygone convexe
N.B: que chaque polygone est définie par un ensemble des points a coordonnées entière.
On trouve sur la toile pas mal d'algorithmes d'intersection de polygones convexes. Le premier que j'ai vu commence par calculer l'enveloppe convexe de la réunion.
J'ai consulté l'algorithme d'Ourke qui permet de calculer l'intersection de deux polygones convexe
mais la problème qui ma rencontré est de déterminée les points d'intersection (leurs coordonnées) et qui ne font pas partie de l'enveloppe convexe des deux polygones !!!
Dans ce cas les points d'intersection identifié par les Pocket lid peuvent ètre de coordonnées non-entière (réels)
malheureusement, c'est pas le cas dans mes recherche !!!
je cherche que les point d'intersection de coordonnées entière si quelqu'un peut m'aider je serai reconnaissant
Merci d'avance.
En général, les sommets de l'intersection de deux polygones convexes à sommets entiers ne sont pas tous entiers !
Que veux-tu dire par : "ce n'est pas la cas dans mes recherches" ? Peux-tu être plus clair ?
Je vous remercie énormément pour votre réponse, tous ce que vous dis est intéressant,
Mais, Monsieur mon thème de recherche concerne les CSPs binaires, je traite des cas particulier des relations binaires, qui définie un problème de satisfaction de contrainte,
représenté sous forme matricielle binaire, semble a des matrice HVDA-convexe (utilisé en tomographie discrète pour des problèmes de reconstruction..)
Mon but essentielle est de faire des opérations d'intersections et de composition sur ses relations.
La distribution des '1' dans les matrices sont sous forme d'un polygone convexe,
donc j'ai besoin de faire l'intersection de deux polygone convexe en un temps de calcul polynomial réduit, en exploitant les propriétés offerte par la notion de convexité.
c'est pour cela que j'ai dit que l'ensemble des points qui définies les polygones sont a coordonnées entière, réellement l'unité me concerne pas.
mais mon but est d'améliorer la complexité d'un algorithme de filtrage(3-consistance) et surtout les opérations de base de cet algorithme (Intersection et Composition)
Une relation HVDA-convexe : si sa représentation matricielle respecte ces
4 conditions à la fois:
-Horizontalement convexe, h-convexe, s'elle est convexe suivant la direction d = (1,0).
-Verticalement convexe, v-convexe, s'elle est convexe suivant la direction d = (0, 1).
-Diagonalement convexe, d-convexe, s'elle est convexe suivant la direction d = (1,1).
-Anti-diagonalement convexe, a-convexe, s'elle est convexe suivant la direction d =( -1, 1)
Si vous pouvez me donner quelque idée pour arriver à faire l'intersection de deux polygones, car c'est la seule shose qui m'enpèche a achever mon but.
Encore je vous remercie énormément pour votre compréhension ainsi que votre réponse.
Je ne sais pas ce que sont les CSP (catégories socio-professionnelles ?) binaires.
Comment sont représentées ces matrices HVDA convexes, quel type de données ?
"temps de calcul polynomial" : polynomial en quoi ? Il me semble que l'algorithme d'intersection le plus bête sera tooujuours poluynomial en la taille des matrices, par exemple. Tu veux dire linéaire ? ou quoi ,
Bref, encore beaucoup de flou.
Bonsoir à tous,
Je n'ai pas compris les explications postées le 14-01-15 à 01:11...
Mais si le problème est de trouver tous les points de coordonnées entières inclus à la fois dans A et dans B (tous deux polygones convexes)...
... alors il y a par exemple la méthode suivante qui est très simple (et qui s'apparente aux algorithmes de coloriage de contours par balayage horizontal) :
1. Pour A, puis pour B, parcourir le contour et identifier les extrêmes pour en déduire R, le rectangle entier minimal contenant A et B.
2. Pour chaque point M de coordonnées entières inclus dans le rectangle R, déterminer si ce point appartient à A et à B respectivement.
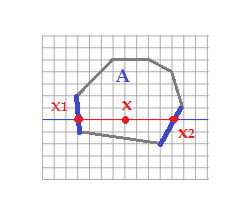
3. Pour déterminer si un point M(x,y) de R appartient au contour polygonal convexe A, il suffit de parcourir les segments de A, et de ne retenir que les deux seuls dont les ordonnées contiennent y. Ceci fait il suffit de calculer pour ces deux segments les abscisses x1 et x2 de leur intersection avec l'horizontale d'ordonnée y du point M. En positionnant x par rapport à x1 et x2, on conclue immédiatement si M est intérieur ou extérieur.
La complexité de l'algorithme est en L*H*N :
L : Largeur horizontale du rectangle (en valeur entière)
H : Hauteur du rectangle (en valeur entière)
N : Nombre de points des contours A et B (qui est aussi le nombre de segments à traiter)
Le traitement est très simple à programmer...
Si la surface du rectangle L*H n'est pas excessive... la méthode est rapide.
Les CSP c'est l'abréviation de Problèmes de satisfaction de contrainte 'Constraint Satisfaction Problem' , c'est un outil de modélisation des problème combinatoire. ces problème sont définie par un ensemble de relations. ceux qui me concerne sont les relations binaires.
Les Matrices HVDA-Convexe sont représenté comme étant un un polygone convexe sur le plan 2D, de façon que chaque M[i,j]=1 correspond à un point x de coordonnées (i,j).
c'est pourquoi je cherche à faire l'intersection de deux polygones convexes au lieu de faire l'intersection de deux matrices car ça sera couteux en temps de calcul.
Le cas de figure que vous avez me donner ne fait pas partie des matrices traité dans mon sujet, car une autre hypothèses est exigé sur les matrices traité dans mon cas d'être des matrice carré, donc le problème décrites en haut par vous ne se pose pas.
Le cas de figure que vous avez me donner ne fait pas partie des matrices traité dans mon sujet, car une autre hypothèses est exigé sur les matrices traité dans mon cas d'être des matrice carré, donc le problème décrites en haut par vous ne se pose pas.
Ici, on ne sait pas à qui tu t'adresses...
Bonsoir Mr LeDino,
Merci pour votre participation,
Pouvez vous m'éclairai le point 1) de votre méthode?
Est ce que le rectangle R correspond a l'enveloppe convexe de la réunion de A et B ?
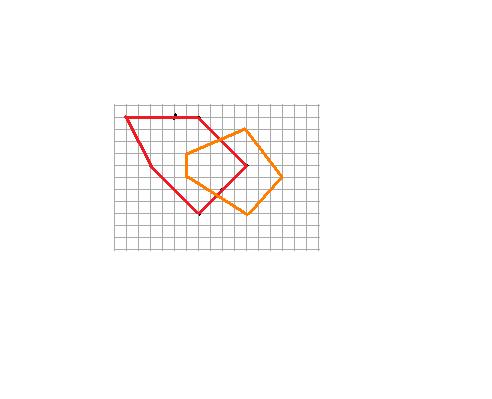
Pas besoin de trouver l'enveloppe convexe.
R est un peu plus grand que l'enveloppe convexe.
Et trouver R, puis parcourir R est ultra simple en programmation.
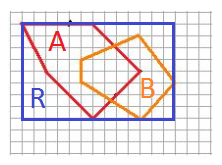
Finalement, en adaptant un tout petit peu le balayage, on peut facilement définir un algorithme de complexité inférieure, en N * min(L,H).
Explication : Pour chaque y fixé, trouver x1 et x2 est simplement en complexité N (car il y a N segments parmi lesquels il faut trouver les deux interceptés par l'horizontale y). Il suffit en effet de calculer x1 et x2 pour les deux segments interceptés et de prendre les valeurs entières immédiatement intérieures à x1 et x2.
Il est donc inutile de balayer en x.
Limem90 :
Le cas de figure que vous avez me donner ne fait pas partie des matrices traité dans mon sujet, car une autre hypothèses est exigé sur les matrices traité dans mon cas d'être des matrice carré, donc le problème décrites en haut par vous ne se pose pas.
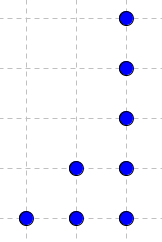
Bien sûr que si : je te l'écris comme matrice carrée :
Est-ce oui ou non une matrice HDVA convexe ? Ca l'est selon la définition que tu as donnée.
Le dessin fait plus haut correspond exactement à cette matrice. Ce n'est pas l'ensemble des points entiers d'un polygone convexe.
J'attends que tu répondes sérieusement à cette objection.
Une matrice HDVA de taille peut être représentée par une liste d'au plus
triplets
(
: n° de ligne où il y a des 1 ;
: premier emplacement sur la ligne où il y a 1 ;
: dernier emplacement sur la ligne où il y a 1).
L'intersection de deux matrices HDVA de taille , dans cette représentation, se calcule facilement en
. Quand on a un triplet
pour la 1e matrice et un triplet
pour la 2e matrice, en posant
et
: si
, prendre
pour l'intersection.
La question de la représentation des matrices HDVA est fondamentale. Tu n'as rien répondu à ma question sur ce sujet.


 géométrie en post-bac
géométrie en post-bac