Inscription / Connexion Nouveau Sujet
intersection deux coubes
bonjour,
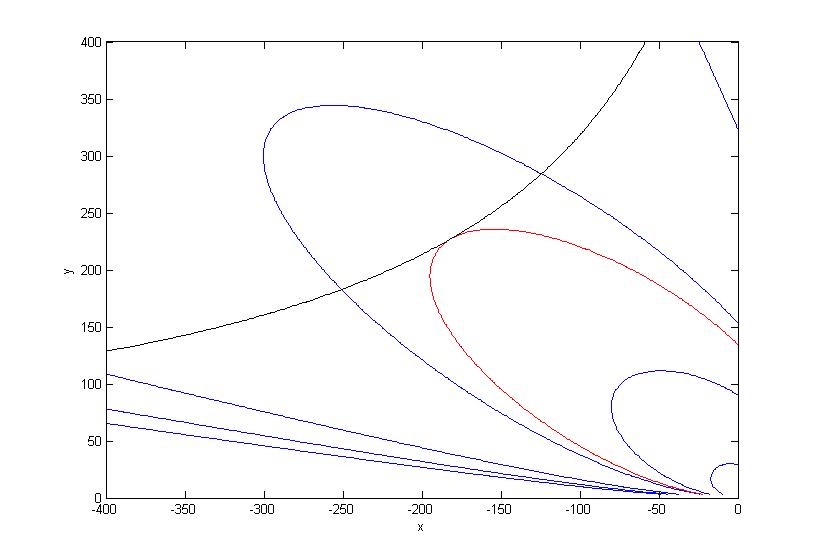
Dans la figure attachée j'ai représenté en noire la courbe d'équation :
A*(B*y+C*x*y)-T=0 avec A,B,C et T des constantes
en bleue j'ai représenté plusieurs courbes d'équation pour différentes valeur de k :
((w*B*y+w*C*x*y)/(R*x^2+R*y^2+w*B*y+w*C*x*y))-k = 0 avec w,B,C etR des constantes.
Je cherche k tel que la courbe noire et l'une des courbes bleues n'ai qu'un seul point en commun.(point d intersection entre la courbe noire et rouge)
J'ai déjà égaliser les deux membres des équations mais le problème est que je me retrouve avec une équation et 2 variables (car x est lié à y par 600^2=x^2+y^2). J'ai les conditions suivantes :
-600<=x<=0 ; 0<=y<=600 et 0,5<k<1.
Je ne vois pas comment résoudre ce problème pouvez-vous m'aider ?
en faite je me suis trompée x et y ne sont pas relié par la relation précédente mais plutot la condition suivante : x^2+y^2<=600^2
bonjour
je ne distingue pas trop les couleurs de tes courbes...
en revanche, vu la nature de tes courbes pour lesquelles tu recherches un seul point commun,
serait-i intéressant de s'intéresser au fait que les courbes sont tangentes en ce point ?
tu aurais alors une relation supplémentaire sur les dérivées...
A creuser peut-être ?

bonjour,
j'ai réfléchis aux tangentes. J'ai les équations de courbes sous la forme suivante :
f(x,y)=0 et gk(x,y)=0
pour la première courbe je peux facilement exprimer y en fonction de x mais pas pour la deuxième. normalement l'égalité de tangente au point a pour deux courbes y=h(x) et y=k(x) se traduit par h'(a)= k'(a). Cela équivaut-il à l'égalité des dérivés df/dx=dg/dx et df/dy=dg/dy pour mon cas ?
Autre approche.
Il faut que le système suivant ait un seul couple de solutions réelles
A*(B*y+C*x*y)-T=0
(w*B*y+w*C*x*y)/(R*x^2+R*y^2+w*B*y+w*C*x*y))-k = 0
A*(B*y+C*x*y)-T=0
y(B+C*x)= T/A
y = T/[A.(B+Cx)]
w*B*y+w*C*x*y = k.(R*x^2+R*y^2+w*B*y+w*C*x*y)
w*y(B+C*x)(1-k) = k.R.(x^2+y^2)
w*T/[A.(B+Cx)]*(B+C*x)(1-k) = k.R.(x^2+[T/(A.(B+Cx))]^2)
w*T(1-k)/A = k.R.(x^2+[T/(A.(B+Cx))]^2)
w*T(1-k)/A = k.R.(x^2+[T²/(A².(B+Cx)²)])
w*T(1-k)*(A².(B+Cx)²) = A.k.R.(x^2*(B+Cx)²+T²)
w*T(1-k)*A.(B+Cx)² = k.R.(x^2*(B+Cx)²+T²)
Il faut donc que cette équation du 4ème degré ait une et une seule solution réelle...
-----
Calculs à vérifier ...

merci beaucoup l'équation est beaucoup plus simple maintenant avec mes conditions je vais tenter de trouver k et x.
je trouve bien l'équation du 4ème degrè suivante :
w*T(1-k)*A.(B+Cx)² = k.R.(x^2*(B+Cx)²*A^2+T²)
le problème c'est que j'ai deux variables réelles : x et k et que je connais juste leur intervalle -600<x<0 et 0<k<1.
je me suis dis alors si les deux membres sont égaux alors leur dérivées par rapport a x doivent etre égale (respectivement pour k) mais ai-je le droit ? Y-a-t'il une méthode à appliquer dans mon cas ?
bonjour
deux fonctions égales n'implique pas leurs dérivées égales
prends le cas de f(x)=x et g(x)=-x en x=0 : elles y sont égales leur dérivées y sont opposées...

w*T(1-k)*A.(B+Cx)² = k.R.(x^2*(B+Cx)²*A²+T²)
f(x) = w*T(1-k)*A.(B+Cx)² - k.R.(x^2*(B+Cx)²*A²+T²)
f '(x) = 2.C.w*T(1-k)*A.(B+Cx) - kR(2x(B+Cx)²A² + 2C.x²(B+Cx).A²)
f '(x) = (B+Cx).[2.C.w*T(1-k)*A - kR(2x(B+Cx)A² + 2C.x².A²)]
On peut donc facilement trouver les 3 solutions de f '(x) = 0 (dont 2 dépendent de k)
Si il y a une seule racine réelle à l'équation w*T(1-k)*A.(B+Cx)² = k.R.(x^2*(B+Cx)²*A²+T²), ce ne peut être qu'à un extremum de f(x) et on doit avoir pour cette valeur de x, la fonction f qui s'annule.
Il faut alors encore vérifier si les valeurs de f pour les 2 autres extrema sont de même signe que la lim(x->+oo) de f(x) ...
-----
Bref, ce devrait être assez facile si on connait les valeurs numériques des constantes w, T, A, B et C et R, mais est asser lourd si on essaie de traiter le problème en trainant ces constantes de manière littérale.
Sauf distraction ou erreur de raisonnement.



 géométrie en post-bac
géométrie en post-bac