Bonjour Mahclaire,

Je vais noter un polygone à côtés,
et la longueur d'un de ses côtés.

"x est inversement proportionnel au nombre de côtés de P"
Autrement dit, on te demande si il existe une constante telle que, pour tout , .

Tu peux commencer par chercher le qui va satisfaire l'égalité ci-dessus pour par exemple, et vérifier si ça marche toujours avec le même pour .
Si ça ne marche pas, alors la propriété du début est fausse...

Pour information,

bonjour

qui se simplifie en :

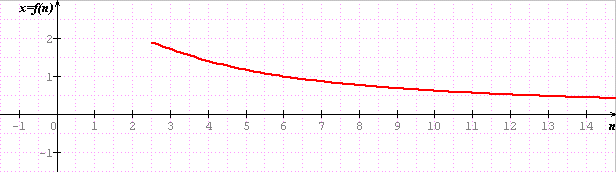
x = V( 2-2cos(2pi/n) )

n=3, x=V3

n=4, x=V2

n=6, x=1

On retrouve les valeurs de l'exo précédent

Merci Delool; comment obtient-on x=f(n) ?

Philoux

Pour calculer dans le cas général, j'utilise le théorème de Pythagore.

Je suppose que le rayon est égal à 1, pour simplifier les calcul.

Sur le dessin, l'angle vaut .
(Donc j'ai oublié le facteur 2 dans ma réponse précédente)

Je calcule :

.

Du coup,
qui se simplifie en

Ps : désolé pour la qualité du dessin, mais c'est la première fois que j'en attache un à mon texte.

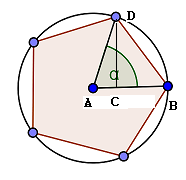
désolé pour la qualité du dessin, mais c'est la première fois que j'en attache un à mon texte.

si toutes les pièces jointes étaient de cette qualité...

Philoux

Merci pour votre aide. Je vais essayer d'y réfléchir à tête reposée.
Cordialement,
Claire

Bonjour;
Si est le rayon du cercle circonscrit au polygone , le nombre de côtés de et la longeur d'un côté on a aussi et comme pour des valeurs assez grandes de on aura donc l'égalité empirique et on voit que ainsi l'inverse proportionnalité de la longeur du côté d'un polygone régulier au nombre de ses côtés est une (vérité empirique).

Salut elhor

le fait de dire n.xn = 2piR consiste à approximer la longueur du côté du polygone (la corde) à la longueur de l'arc

La réponse à la question de Claire
L'affirmation suivante est-elle vraie : x est inversement proportionnel au nombre de côtés de P ?
est-elle bien "non" ?

A lire ton dernier post, le doute m'envahit...

Philoux