Inscription / Connexion Nouveau Sujet
Isométrie du plan / nombre complexe / Suite
Bonjour,
Soit P plan orienté rapporté à (0, ,
, ) orthonormal direct, M d'affixe Z,
) orthonormal direct, M d'affixe Z,
f(M) = M' d'affixe Z' = -jZ + i où j = ei(2 /3)
/3)
1. Trouver la nature et les éléments caractéristiques de f.
2. Soit la suite de point (Mn)n
 , définie par :
, définie par :
M0
et
pour tout n de  , Mn+1 = f (Mn)
, Mn+1 = f (Mn)
L'affixe de Mn est Zn et l'affixe de Mn+1est Zn+1=-jZn + i
a. On pose Zn= Zn - ei( /6)
/6)
Calculer Zn+1 en fonction de Zn, puis de Zn en fonction de n.
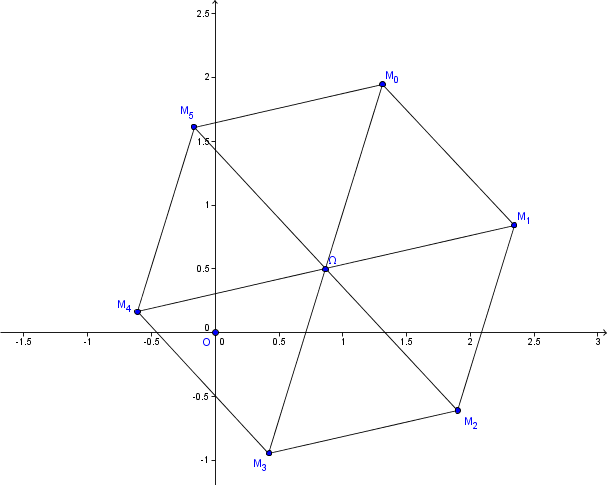
b. Représenter graphiquement les points: M0, M1, M2, M3, M4, M5 et M1989
Bonjour,
1)
avec
C' est une rotation d' angle
Son centre est sont point fixe:
est donc la rotation de centre
et d' angle

Bonjour,
cailloux, est-ce que vous avez intégré i dans la conclusion et comment faire la schématisation à partir d'un exemple ?
Merci encore.
Une fôte de frappe à la première ligne; il faut lire:
Ce qui ne change rien pour la suite.
2)a) Ton énoncé ne tient pas la route....
2)b)

Bonjour,
Merci pour vos réponses, qui ont aidé.
En effet à vérifier:
La représentation géométrique:
Z3 égal=, quand le signe -reste à i
1) =( + 5
+ 5 /6) et faire la symétrie par rapport à l'axe des x à partir du nouveau centre
/6) et faire la symétrie par rapport à l'axe des x à partir du nouveau centre  .
.
2) =, en intégrant le signe -, il n'aura pas besoin d'effectuer la symétrie (i, c'est partie imaginaire sin)
O est distant de longueur module ||i|| du point invariant  (translation i)
(translation i)
A bientôt.

 !!!
!!!
