Inscription / Connexion Nouveau Sujet
Isométrie et point fixe
Bonjour,
Soit O et O' deux points distincts du plan, g une rotation de centre O d'angle non nul 
. On considère l'isométrie f = t o g.
Soit N un point du plan tel que (OO,ON) 
/2 - /2 [2], N' son image par g.
L'image de la droite (ON) par la translation t coupe (ON') en un point B.
En considérant l'antécedent de B par g, montrer que f possède un point fixe.
Merci d'avance.
ah, c'est toute la question
d'abord, ta figure ne me semble pas respecter l'énoncé
O, O' distincts : OK
angle non nul : il est matérialisé où sur la figure ?
g : rotation de centre O, d'angle
t : translation de vecteur
f : composée de g puis de t :
La théorie dit que f est une rotation d'angle
Cet exercice propose une manière de "construire" le centre de la rotation f.
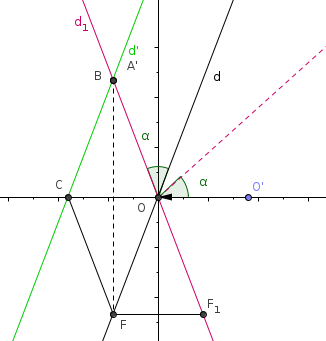
Pour cela, on considère la droite d, image de la droite (OO') par une autre rotation, de centre O, d'angle
puis la droite d', image de d par la translation t
et la droite , image de d par la rotation g
B intersection de d' et
Je rajoute
C intersection de d' et de (OO')
F symétrique de B par rapport à (OO')
Montre maintenant que , image de F par g, est sur
et que l'image de par t est ... F
utilise pour cela les angles sur le schéma, les propriétés des figures vues en petites classes.
C'est de la géométrie de papa, ça.
Annuler
connectez vous