Inscription / Connexion Nouveau Sujet
Je suis Bloqué 
Bonjour, à tous & à toutes.
Sujet : Fonction Exponentielle
Je vous demande de l'aide pour la partie A d'un exercice, trouver une solution à ce problème pourrai, m'aider à mieux comprendre, si d'autres exercices de se genre se présente lors d'une évaluation.
A) Problème :
Une fibre optique est jugée performante lorsque, sur une longueur donnée, la puissance du signal qu'elle transmet subit une perte minimale. Pour un signal d'entrée de puissance fixée, la puissance lumineuse à la sortie d'une fibre optique dépend de sa longueur L. Cette puissance de sortie Ps est modélisée par la formule suivante, où Ps est la puissance en milliwatts (mW) et L la longueur en kilomètres (km):
PS = 5,2e(- 0,18L)
Lorsque le signal perd 85 % de sa puissance, il nécessite une amplification.
Problématique : au bout de combien de kilomètres le signal transmis par la fibre doit-il être amplifié ?
Méthode graphique :
On considère la fonction f définie sur l'intervalle [0 ; 15] par f(x) = 5,2e(- 0,18L)
1.1 ▪ Calculer f (0) et f (15).
1.2 ▪ Calculer f '(x) où f ' désigne la dérivée de f.
1.3 ▪ Déterminer le signe de f '(x) sur l'intervalle [0 ; 15]. Justifier la réponse.
1.4 ▪ En déduire le sens de variation de f et compléter le tableau de variation ci-dessous sur votre feuille.
| x | 0 | 15 |
| Signe de f'(x) | ||
| Variationsde f |
1.5 ▪ Tracer à la calculatrice ou avec Geogebra la courbe représentative de f sur l'intervalle [0 ; 15].
1.6 ▪ En utilisant la calculatrice ou l'ordinateur et les informations de l'énoncé, répondre à la problématique et donner votre résultat arrondi à 0,01 près. Justifier et expliquer clairement chaque étape de votre démarche. (vous pouvez aussi utiliser la méthode de résolution d'équation plutôt que la méthode graphique)
Cordialement,
Hugo.
TERA
Bonjour,
Je bloque pour la résolution de se problème, Nommé "A".
Cette exercice nous a été donné et je suis bloqué malheureusement sur ce dernier, la deuxième partie de cet exercices, je l'ai résolu mais cette première partie "A". Impossible de comprendre sans réponse.
C'est la première fois que nous sommes sur cette leçons. Donc c'est inconnu pour moi. Je voudrai connaître quelque réponse pour être d'avantage présent pour de prochain contrôle à se sujet.
Regarde là ![]() Fonction exponentielle
Fonction exponentielle
Tu auras les infos et des exos sur la fonction exponentielle
Bonjour à toi
Voici ce que j'ai fait pour trouver les réponses c'est plutôt cohérent donc je te l'envoie :
1) pour trouver f(0)et f(15) tu remplace Le par o puis par 15
2) pour trouver f' je me suis appuyé des deux formules suivantes:
UV=U'*V+V'*U
e^(V)=V'e^(V)
(Si la puissance ne s'affiche pas c'est le ^ et ce qui suit qui fait office de puissance
3)f'0 tu vas pas trouver de solution donc elle est continue tu remplace L par un chiffre entre 0et15 est tu obtiens le signe
4)ça tu peux répondre même sans avoir rien fait :vu que la fibre est moins efficace quand elle est longue tu en déduit que la fonction est tjr décroissante
5) c'est pas réellement une question
6) là il faut faire un balayage
Rappel 85%<=>0,85
Et voilà en espérant que
je t'ai été utile
Bonjour
Je suis bloquée sur le même exercice : pouvez-vous m'aider svp ?
Aujourd'hui 80 % du trafic mondial longue distance se fait par des fibres optiques. Ces
dernières ont en effet de multiples avantages par rapport aux câbles électriques
classiques. Elles offrent la possibilité de transmettre des données, de la voix, des
images… à de très hauts débits. Une fibre optique est jugée performante lorsque, sur
une longueur donnée, la puissance du signal qu'elle transmet subit une perte minimale.
Pour un signal d'entrée de puissance fixée, la puissance lumineuse à la sortie d'une
fibre optique dépend de sa longueur 𝐿. Cette puissance de sortie 𝑃𝑆 est modélisée par
la formule suivante :
𝑃𝑆 = 5 𝑒
(−0,2𝐿)
Où 𝑃𝑆 est la puissance en milliwatts (mW) et 𝐿 la longueur en kilomètres (𝑘𝑚). Lorsque
le signal perd 90 % de sa puissance, il nécessite une amplification.
Problématique : au bout de combien de kilomètres le signal transmis par la fibre
doit-il être amplifié ?
1. Méthode graphique :
On considère la fonction 𝑓 définie sur l'intervalle [0 ; 13] par 𝑓(𝑥) = 5𝑒
(-0,2𝑥)
1.1 Calculer 𝑓 (0) et 𝑓 (13).
…………………………………………………………………………………………………
………….………………………………………………………………………………………
…………………….……………………………………………………………………………
……………………………….
1.2 Calculer 𝑓 '(𝑥) où 𝑓 ' désigne la dérivée de 𝑓.
…………………………………………………………………………………………………
………….………………………………………………………………………………………
…………………….……………………………………………………………………………
………………………
Exercices (type CCF) T BAC
A faire et à envoyer avant 10/05/2020 04/05/2020
---------------------------------------------------------------------------------------------------------------------------
2
1.3 Déterminer le signe de 𝑓 '(𝑥) sur l'intervalle [0 ; 13]. Justifier la réponse.
…………………………………………………………………………………………………
………….………………………………………………………………………………………
…………………….……………………………………………………………………………
……………………………….…………………………………………………………………
………………………………
1.4 En déduire le sens de variation de 𝑓 et compléter le tableau de variation cidessous.
𝑥 0 13
Signe de 𝑓′(𝑥)
Variation de 𝑓
1.5 Tracer à la calculatrice ou avec Geogebra la courbe représentative de 𝑓 sur
l'intervalle [0 ; 13].
(Prendre en photo ton travail sur la calculatrice)
1.6 En utilisant la courbe, la calculatrice ou l'ordinateur et les informations de
l'énoncé, répondre à la problématique. Justifier et expliquer votre démarche.
Donner le résultat arrondi à 0,01 près.
…………………………………………………………………………………………………
………….……………………………………………………………………………………
Par avance MERCI
Oui merci je l'ai lu mais je suis bloquée au 1.6 à la fin
Je n'y arrive pas sur la calculatrice ni geogebra du coup je me demande si ce que j'ai fait avant est correct
Bonjour et merci pour votre aide
C'est ça je n'arrive pas à tracer la courbe sur ma calculatrice ni sur geogebra
Comment avez-vous fait svp ?
Pour GeoGebra
vous écrivez dans la barre de saisie g(x)=5 exp(-0.2*x) puis entrée
ensuite f(x)= fonction (g ,0,13) là il suffit plutôt de compléter ce que le logiciel vous propose
Il y a une autre méthode pour tracer directement sur l'intervalle mais je ne m'en souviens plus
J'obtiens donc cela 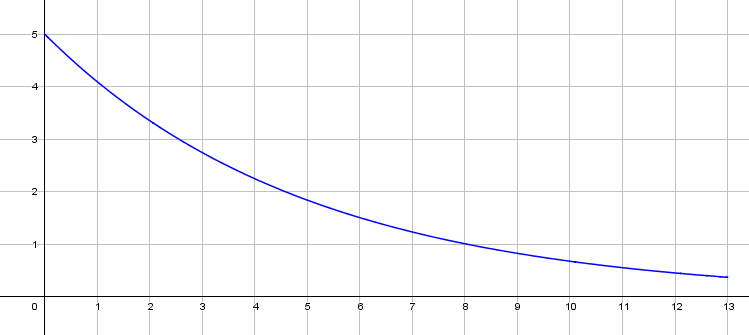
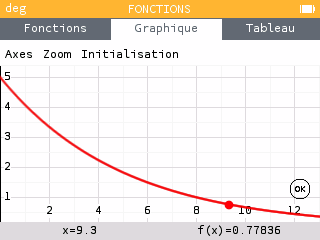
Quant à la calculatrice, comme vous n'avez pas dit sur laquelle vous travaillez, je ne peux répondre.
Deux petites remarques
vous auriez dû ouvrir votre propre sujet car si la trame est la même les valeurs données sont toutes différentes
Vous auriez dû préciser ce qui vous gênait pour répondre, vous auriez peut-être eu une réponse plus rapide.
De rien


 Fonction Exponentielle en terminale
Fonction Exponentielle en terminale